A. Energi Potensial Gravitasi

Energi potensial gravitasi adalah energi yang timbul di antara dua benda akibat gaya tarik gravitasi satu sama lain.

\(U = - \dfrac {M \:.\: m}{r}\)

Nilai energi potensial gravitasi \(U \leq 0\)

Penjelasan mengenai tanda (−) pada energi potensial gravitasi

Bentuk lain dari energi potensial gravitasi adalah \(EP = mgh\), dan rumus tersebut memiliki tanda (+). Rumus \(EP = mgh\) menggunakan kerangka acuan permukaan bumi.

Energi potensial gravitasi dengan rumus \(U = - \dfrac {M \:.\: m}{r}\) digunakan untuk jarak yang sangat besar (alam semesta) dan menggunakan kerangka acuan tak berhingga.

Kedua rumus \(EP = mgh\) dan \(U = - \dfrac {M \:.\: m}{r}\) memiliki arti yang sama.

B. Escape Velocity

Escape velocity adalah kecepatan minimum yang dibutuhkan untuk dapat lepas dari gravitasi bumi.

Misalkan sebuah roket yang akan diluncurkan dari permukaan bumi ke luar angkasa. Dibutuhkan usaha luar dari roket untuk membebaskan diri dari gravitasi bumi.

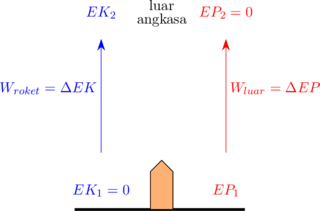
\begin{equation*} \begin{split} W_{\text{roket}} & = W_{\text{luar}}  \\\\ \Delta EK & =  \Delta EP \\\\ EK_2 - EK_1 & = EP_2 - EP_1 \\\\ EK_2 - 0 & = 0 - EP_1 \\\\ EK_2 & = - EP_1 \\\\ \frac 12 \:.\: \cancel {m} \:.\: v^2 & = G \: \frac {M \:.\: \cancel {m}}{R} \quad \dotso \text{ m = massa roket}\\\\ v^2 & = \sqrt{\frac {2GM}{R}} \quad \dotso \text{ M = massa bumi} \end{split} \end{equation*}