Metode Jajaran Genjang
Jumlah dan selisih dua vektor juga dapat ditentukan dengan metode jajaran genjang.
Diketahui dua buah vektor \(\overrightarrow a\) dan \(\overrightarrow b\) saling membentuk sudut \(\theta\) seperti gambar di bawah ini:
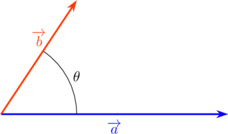
(A) resultan kedua vektor \(\overrightarrow a + \overrightarrow b\)
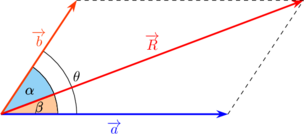
\( R = |a + b| = \sqrt{a^2 + b^2 + 2 \: a \: b \cos \theta}\)
\(\dfrac{|a|}{\sin \alpha} = \dfrac{|b|}{\sin \beta} = \dfrac{|R|}{\sin \theta}\)
(B) selisih kedua vektor \(\overrightarrow a - \overrightarrow b\)
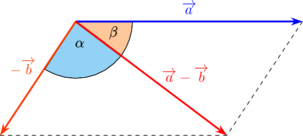
\( |a - b| = \sqrt{a^2 + b^2 - 2 \: a \: b \cos \theta}\)
\(\dfrac{|a|}{\sin \alpha} = \dfrac{|b|}{\sin \beta} = \dfrac{|a - b|}{\sin \theta}\)
SOAL LATIHAN
