| Grafik | Keterangan |
|---|---|
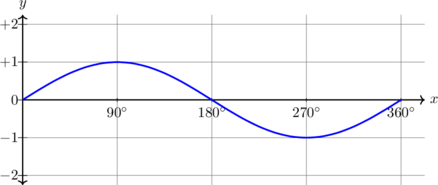
| \(y = \sin x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(360^\text{o}\)
Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
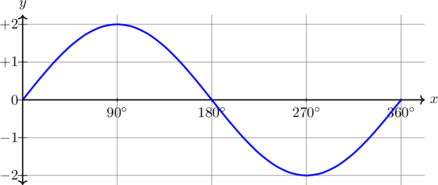
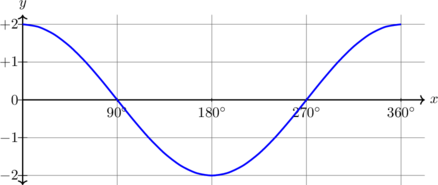
| \(y = 2 \sin x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperbesar 2 kali dalam arah Y
Periode = \(360^\text{o}\) Amplitudo = 2 \(y_{\text{max}} = 2\) \(y_{\text{min}} = -2\) |
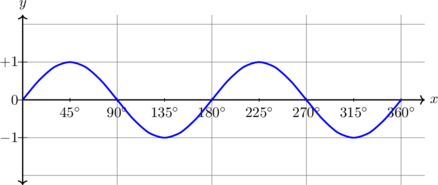
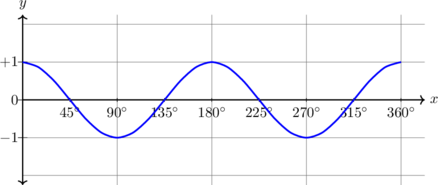
| \(y = \sin 2x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperkecil \(\dfrac 12\) kali dalam arah X
Periode = \(\dfrac {360^{\text{o}}}{2} = 180^{\text{o}}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
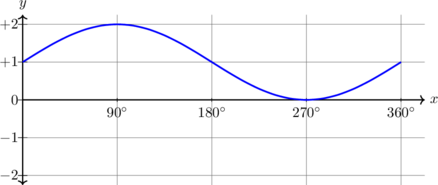
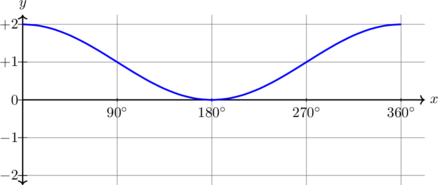
| \(y = \sin x + 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke atas
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 2\) \(y_{\text{min}} = 0\) |
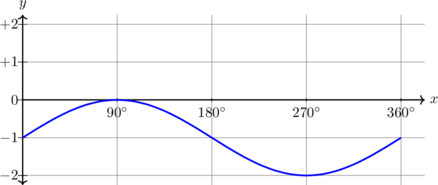
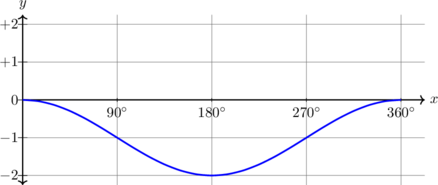
| \(y = \sin x - 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke bawah
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 0\) \(y_{\text{min}} = -2\) |
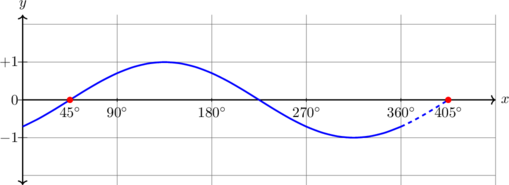
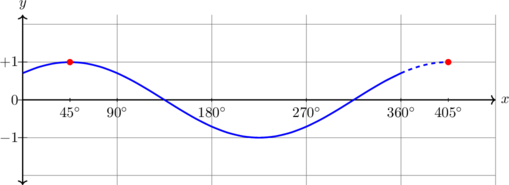
| \(y = \sin (x - 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kanan
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
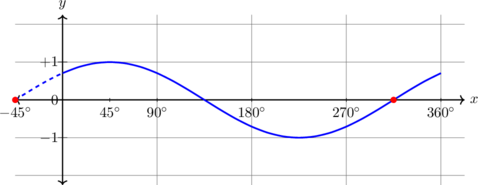
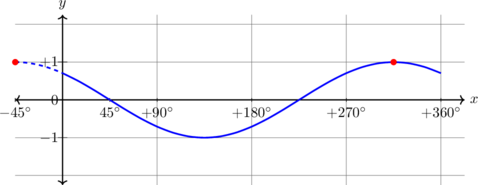
| \(y = \sin (x + 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kiri
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| Grafik | Keterangan |
|---|---|
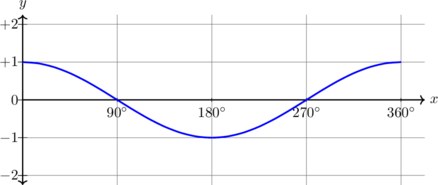
| \(y = \cos x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(360^\text{o}\)
Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| \(y = 2 \cos x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperbesar 2 kali dalam arah Y
Periode = \(360^\text{o}\) Amplitudo = 2 \(y_{\text{max}} = 2\) \(y_{\text{min}} = -2\) |
| \(y = \cos 2x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperkecil \(\dfrac 12\) kali dalam arah X
Periode = \(\dfrac {360^{\text{o}}}{2} = 180^{\text{o}}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| \(y = \cos x + 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke atas
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 2\) \(y_{\text{min}} = 0\) |
| \(y = \cos x - 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke bawah
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 0\) \(y_{\text{min}} = -2\) |
| \(y = \cos (x - 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kanan
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| \(y = \cos (x + 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kiri
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| Grafik | Keterangan |
|---|---|
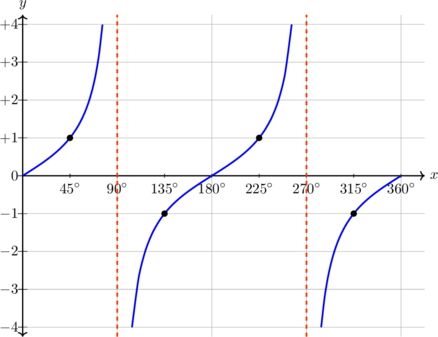
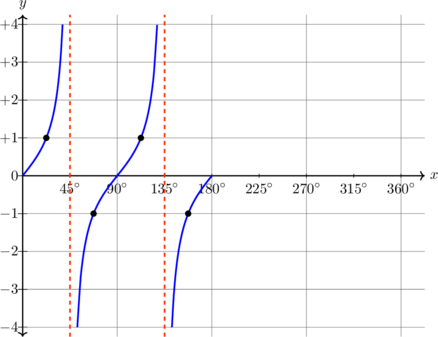
| \(y = \tan x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(180^\text{o}\)
Pada x = 45º, y = 1
|
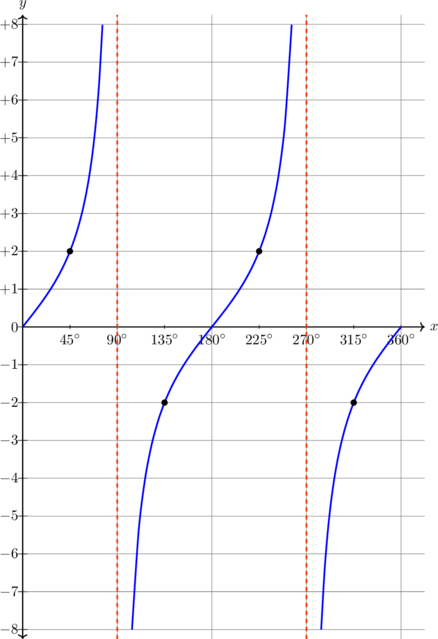
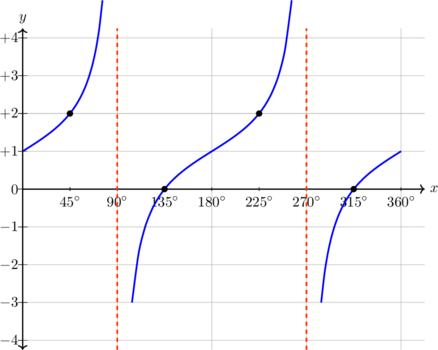
| \(y = 2 \tan x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(180^\text{o}\)
Pada x = 45º, y = 2 |
| \(y = \tan 2x, \quad 0^\text{o} \leq x \leq 180^\text{o}\)
|
Periode = \(\dfrac {180^{\text{o}}}{2} = 90^{\text{o}}\)
Pada x = 22.5º, y = 1 |
| \(y = \tan x + 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke atas
Periode = \(180^\text{o}\) Pada x = 45º, y = 2
|
| \(y = \tan x - 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke bawah
Periode = \(180^\text{o}\) Pada x = 45º, y = 0 |
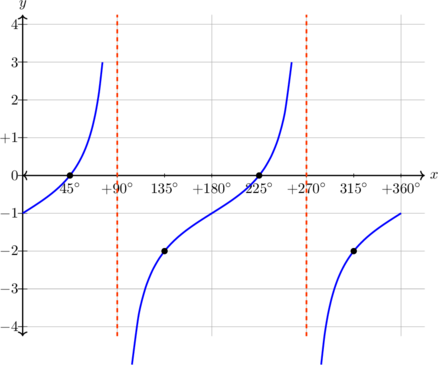
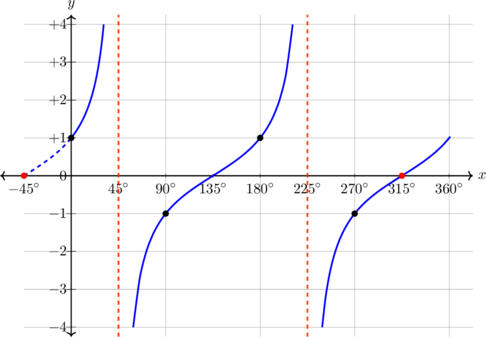
| \(y = \tan (x - 45), \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kanan
Periode = \(180^\text{o}\) Pada x = 90º, y = 1 |
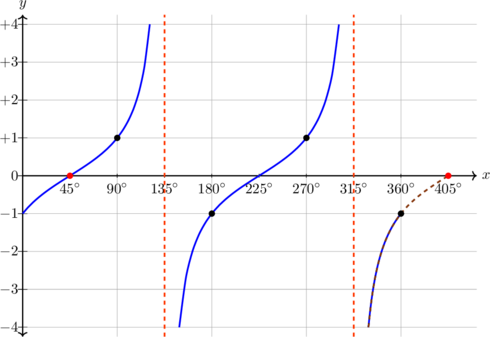
| \(y = \tan (x + 45), \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kiri
Periode = \(180^\text{o}\) Pada x = 0º, y = 1 |
SOAL LATIHAN
Sketsa grafik \(y = 3 \sin (2x + 60^{\text{o}}) - 1\), \(0^{\text{o}} \leq x \leq 360^{\text{o}}\) dan kemudian tentukan:
(A) Amplitudo
(B) Periode
(C) Nilai maksimum dan minimum fungsi
Pembahasan:
Sketsa grafik \(y = 1 - 2 \sin (3x - \frac 12 \pi)\), \(0 \leq x \leq 2 \pi\) dan kemudian tentukan:
(A) Amplitudo
(B) Periode
(C) Nilai maksimum dan minimum fungsi
Pembahasan: