Discriminant
\(D = b^2 - 4ac\)
\(D > 0\), two distinct real roots
\(D = 0\), one real root/two coincident roots/repeated root
\(D < 0\), no real root (imaginary roots)
Example
Given quadratic equation \(2x^2 - 5x - 3= 0\)
A. Determine the discriminant
B. State the nature of its roots
A. Discriminant
\begin{equation*} \begin{split} D & = b^2 - 4ac \\\\ D & = (-5)^2 - 4(2)(-3)\\\\ D & = 49 \end{split} \end{equation*}
B. Nature of roots
Since \(D > 0\), the equation has two distinct real roots.
Definite Form
Positive Definite
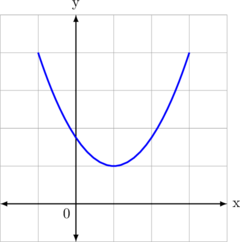
\(a^2 + bx + c > 0\)
Condition:
\(a > 0\) and \(D < 0\)
Since the curve is concave up, then \(a > 0\)
Since the curve does not cut x axis, then \(D < 0\)
Negative Definite
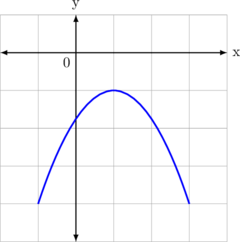
\(a^2 + bx + c < 0\)
Condition:
\(a < 0\) and \(D < 0\)
Since the curve is concave down, then \(a < 0\)
Since the curve does not cut x axis, then \(D < 0\)
Exercise
