Related Angles
1. Quadrant
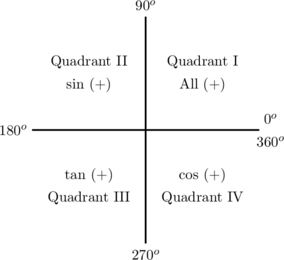
2. Use of 90º, 180º, 270º and 360º
| 90º and 270º | 180º and 360º | ||
| \(\sin (90 - \alpha) = \cos \alpha\) | \(\sin (90 + \alpha) = \cos \alpha\) | \(\sin (180 - \alpha) = \sin \alpha\) | \(\sin (180 + \alpha) = - \sin \alpha\) |
| \(\sin (270 - \alpha) = -\cos \alpha\) | \(\sin (270 + \alpha) = -\cos \alpha\) | \(\sin (360 - \alpha) = - \sin \alpha\) | \(\sin (360 + \alpha) = \sin \alpha\) |
| \(\cos (90 - \alpha) = \sin \alpha\) | \(\cos (90 + \alpha) = - \sin \alpha\) | \(\cos (180 - \alpha) = - \cos \alpha\) | \(\cos (180 + \alpha) = - \cos \alpha\) |
| \(\cos (270 - \alpha) = - \sin \alpha\) | \(\cos (270 + \alpha) = \sin \alpha\) | \(\cos (360 - \alpha) = \cos \alpha\) | \(\cos (360 + \alpha) = \cos \alpha\) |
| \(\tan (90 - \alpha) = \cot \alpha\) | \(\tan (90 + \alpha) = - \cot \alpha\) | \(\tan (180 - \alpha) = - \tan \alpha\) | \(\tan (180 + \alpha) = \tan \alpha\) |
| \(\tan (270 - \alpha) = \cot \alpha\) | \(\tan (270 + \alpha) = - \cot \alpha\) | \(\tan (360 - \alpha) = - \tan \alpha\) | \(\tan (360 + \alpha) = \tan \alpha\) |
3. Bigger Angles
For bigger angles, we must find the remainder angles after multiplication of 360°.
Example
\begin{equation*} \begin{split} \sin 1470^{\text{o}} & = \sin (360^{\text{o}} \:.\: 4 + 30^{\text{o}}) \\\\ \sin 1470^{\text{o}} & = \sin 30^{\text{o}} \\\\ \sin 1470^{\text{o}} & = \frac{1}{2} \end{split} \end{equation*}
4. Negative Angles
Negative angles can be assumed that the angle is on the 4th quadrant.
\(\sin (- \alpha) = - \sin \alpha\)
\(\cos (- \alpha) = \cos \alpha \)
\(\tan (- \alpha) = - \tan \alpha \)
Exercise
