Tangent and Normal

Differentiation

Tangent and Normal

Rendered by QuickLaTeX.com

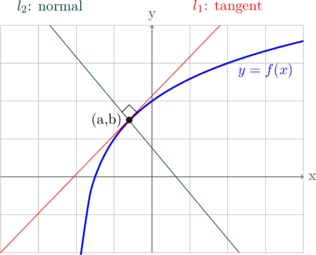
Tangent

Equation of tangent to the curve $y = f (x)$ at $(a, b)$ can be determined by:

(1) Gradient of tangent

$m = y^{'} = f^{'} (a)$

(2) Equation of tangent

$y - y_{1} = m . (x - x_{1})$

Normal

Normal is perpendicular line to the tangent at the same point.

Equation of normal to the curve $y = f (x)$ at $(a, b)$ can be determined by:

(1) Gradient of tangent

$m = y^{'} = f^{'} (a)$

(2) Gradient of normal

$m_{t} . m_{n} = - 1$

(2) Equation of normal

$y - y_{1} = m_{n} . (x - x_{1})$

Example 01

Determine equation of tangent and normal to the curve $f (x) = x^{3} + 4 x^{2} - 5 x + 1$ at $(1, 2)$ .

Tangent

Gradient of tangent at (1,2)

$\begin{aligned} f (x) = x^{3} + 4 x^{2} - 5 x + 1 \\ f^{'} (x) = 3 x^{2} + 8 x - 5 \\ f^{'} (1) = 3 (1)^{2} + 8 (1) - 5 \\ m_{t} = 6 \end{aligned}$

Equation of tangent at (1,2)

$\begin{aligned} y - y_{1} = m_{t} . (x - x_{1}) \\ y - 2 = 6 . (x - 1) \\ y - 2 = 6 x - 6 \\ y = 6 x - 4 \end{aligned}$

Normal

Gradient of normal at (1,2)

$\begin{aligned} m_{t} \times m_{n} = - 1 \\ 6 \times m_{n} = - 1 \\ m_{n} = - \frac{1}{6} \end{aligned}$

Persamaan garis normal di titik (1,2)

$\begin{aligned} y - y_{1} = m_{n} . (x - x_{1}) \\ y - 2 = - \frac{1}{6} . (x - 1) \\ y - 2 = - \frac{1}{6} x + \frac{1}{6} \\ y = - \frac{1}{6} x + 2 \frac{1}{6} \end{aligned}$

Exercise

--- Open this page ---