Domain and Range
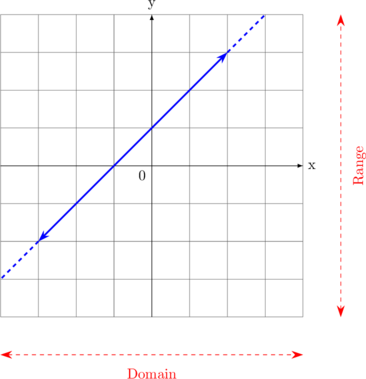
| A. Linear Function | |
|---|---|
| \(y = mx + c\)
|
Domain
\(- \sim \: < x < \: \sim\)
Range \(- \sim \: < y < \: \sim\) |
|
B. Quadratic Function |
|
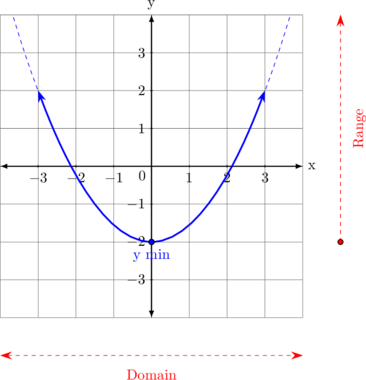
| Concave up
\(y = ax^2 + bx + c, \: a > 0\)
|
Domain
\(- \sim \: < x < \: \sim\)
Range \(\{y \geq y_{\text{min}}\}\)
Determine extreem value \(x_p = - \dfrac {b}{2a}\) Substitute \(x_{\text{p}}\) into the equation to find \(y_p\) |
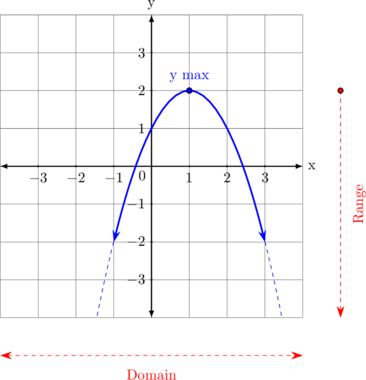
| Concave down
\(y = ax^2 + bx + c, \: a < 0\)
|
Domain
\(- \sim \: < x < \: \sim\)
Range \(\{y \leq y_{\text{max}}\}\) |
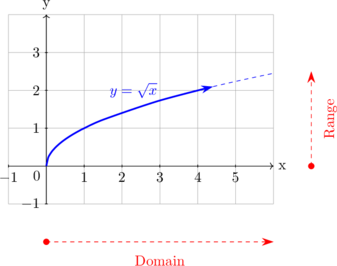
| C. Root Function | |
| \(y = \sqrt{x}\)
|
Domain
\(x \geq 0\)
Range \(y \geq 0\) |
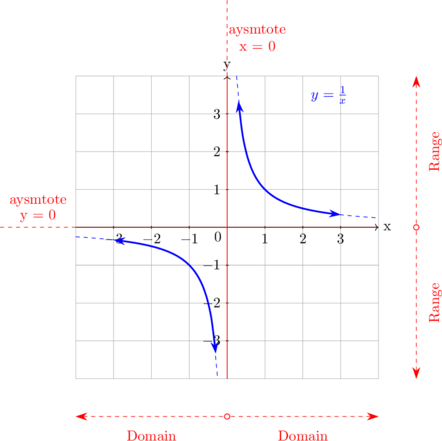
| D. Rational Function | |
| \(y = \dfrac 1x\)
|
Horizontal Asymtote
\(y = 0\)
Vertical Asymtote \(x = 0\)
Domain \(\{x \neq 0\}\)
Range \(\{y \neq 0\}\) |
Exercise