Uniform Acceleration
Characteristics of Uniform Acceleration
- Value of velocity changes in time linearly
- Acceleration ≠ 0, it can be positive (accelerated) or negative (decelerated)
Formula
\begin{equation*} \begin{array} {lll} & s = v_\text{o} \:.\: t + \frac{1}{2} \:.\: a \:.\: t^2 \quad & (1) \\\\ & v_\text{t} = v_\text{o} + a \:.\: t \quad & (2) \\\\ & v_\text{t}^2 = v_\text{o}^2 + 2 \:.\: a \:.\: s \quad & (3) \end{array} \end{equation*}
- \(s\) = distance (m)
- \(v_{\text{o}}\) = initial velocity (m/s)
- \(v_{\text{t}}\) = final velocity (m/s)
- \(a\) = acceleration (m/s2)
- Accelerated \(a = (+)\)
- Decelerated \(a= (-)\)
- \(t\) = waktu (s)
Graph
s vs t
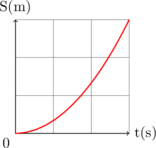
v vs t
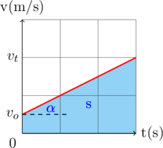
\(s\) = area under curve
\(a = \tan \alpha\)
a vs t
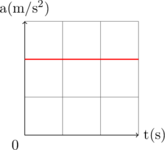
Exercise
