Getaran pada Bandul

Mula-mula benda diposisikan pada titik A lalu dilepaskan sehingga benda akan berayun. Jika diasumsikan tidak ada hambatan udara dan gesekan lainnya, maka benda akan bergetar harmonis. Waktu yang dibutuhkan dari posisi A ke posisi B sama dengan waktu yang dibutuhkan dari posisi B ke posisi C. Demikian juga sebaliknya.
Periode dan frekuensi bandul
Satu getaran adalah 1 getaran bolak-balik, yaitu dari posisi A − B − C − B − A. Waktu yang dibutuhkan untuk 1 getaran (A − B − C − B − A) disebut periode (T).
\(T = 2 \pi \sqrt {\dfrac {l}{g}}\)
\(f = \dfrac {1}{2 \pi} \sqrt {\dfrac {g}{l}}\)
l = panjang tali
g = percepatan gravitasi
Simpangan dan Amplitudo
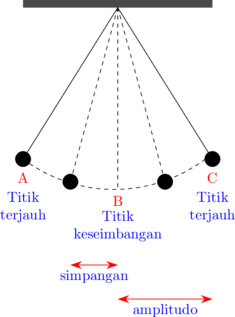
Titik B merupakan titik seimbang
Titik A dan C merupakan titik terjauh
Jarak dari titik seimbang ke posisi benda pada waktu tertentu disebut simpangan.
Jarak dari titik seimbang ke titik terjauh (jarak B - A atau jarak B - C) disebut amplitudo.
Getaran pada Pegas
Periode dan frekuensi pegas
Saat benda bergetar dari posisi A menuju B, berbalik menuju C dan kemudian berbalik lagi menuju A disebut satu getaran. Waktu yang dibutuhkan untuk satu getaran disebut periode (T).
\(T = 2 \pi \sqrt {\dfrac {m}{k}}\)
\(f = \dfrac {1}{2 \pi} \sqrt {\dfrac {k}{m}}\)
m = massa benda
k = konstanta pegas
Simpangan dan Amplitudo
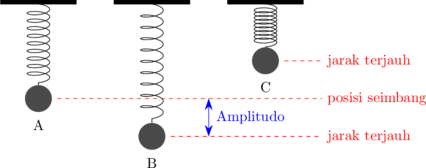
Titik A merupakan titik seimbang
Titik B dan C merupakan titik terjauh
Jarak dari titik seimbang ke titik terjauh (jarak A - B atau jarak A - C) disebut amplitudo.
SOAL LATIHAN
