Gelombang adalah rambatan (aliran) energi yang berpindah dari satu tempat ke tempat lainnya.

 

Berdasarkan arah rambatannya, gelombang dibedakan menjadi:

1. Gelombang transversal

− Arah rambatan gelombang tegak lurus dengan arah getaran.

 

 

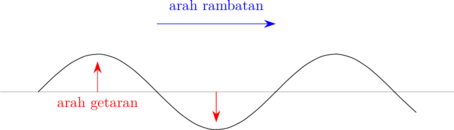
− Terdapat bukit gelombang dan lembah gelombang.

 

 

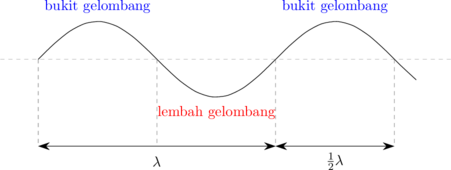
− Satu panjang gelombang (λ) adalah jarak antara satu regangan dan satu rapatan.

 

− Contoh: gelombang pada tali, gelombang laut, sinar matahari, gelombang elektromagnetik.

 

 

2. Gelombang longitudinal

− Arah rambatan gelombang sejajar dengan arah getaran.

 

 

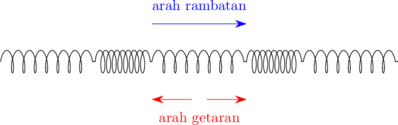
− Terdapat regangan dan rapatan.

 

 

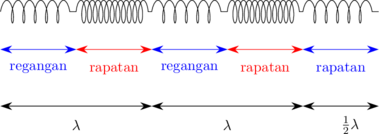
− Satu panjang gelombang (λ) adalah jarak antara satu regangan dan satu rapatan.

 

− Contoh: gelombang bunyi, gelombang pada pegas/slinki.

 

 

Berdasarkan arah mediumnya, gelombang dibedakan menjadi:

1. Gelombang mekanik

− gelombang yang membutuhkan medium untuk merambat

− contoh: gelombang pada tali, gelombang laut, sinar matahari, gelombang bunyi

 

2. Gelombang elektromagnetik

− gelombang yang tidak membutuhkan medium untuk merambat

− contoh: sinar matahari, gelombang radio, gelombang pada telepon selular

 

 

Cepat rambat gelombang

Gelombang adalah energi yang merambat/mengalir. Kecepatan gelombang merambat dapat ditentukan sebagai berikut:

 

Kurva gelombang dapat dinyatakan dengan diagram cartesius sebagai simpangan vs jarak dan simpangan vs waktu

 

Kurva y vs x

 

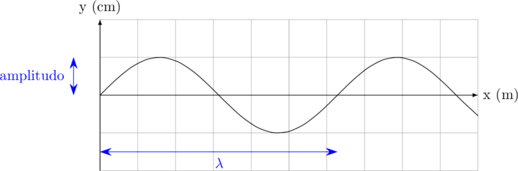
Kurva y vs t

 

 

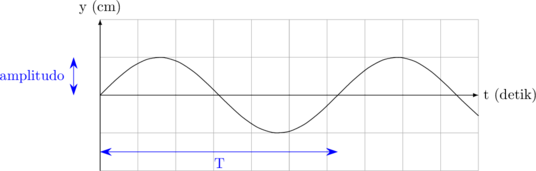
Simpul dan perut gelombang

 

 

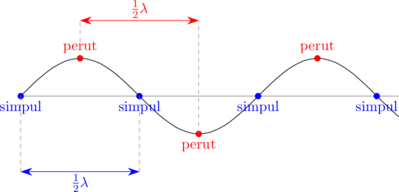
Jarak antara dua simpul berdekatan adalah \(\frac 12 \lambda\). Maka setiap jarak \(\frac 12 \lambda\) terdapat dua simpul.

 

Jarak antara dua perut berdekatan adalah \(\frac 12 \lambda\). Maka setiap jarak \(\frac 12 \lambda\) terdapat dua perut.

 

Jarak antara simpul dan perut yang berdekatan adalah \(\frac 14 \lambda\).