A. Cepat Rambat Gelombang Bunyi
Pada zat padat
\(v = \sqrt{\dfrac {E}{\rho}}\)
Pada zat cair
\(v = \sqrt{\dfrac {B}{\rho}}\)
Pada zat gas
\(v = \sqrt{\gamma \:.\: \dfrac {P}{\rho}}\)
\(v = \sqrt{\gamma \:.\: \dfrac {R \:.\: T}{M}}\)
v (zat padat) > v (zat cair) > v (zat gas)
B. Interferensi
Konstruktif (kuat)
\(\Delta s = n \:.\: \lambda\)
\(n = 0, 1, 2, 3, \dotso\)
Destruktif (lemah)
\(\Delta s = (n + \frac 12) \:.\: \lambda\)
\(n = 0, 1, 2, 3, \dotso\)
C. Efek Doppler
\(f_p = \dfrac {v \pm v_p}{v \pm v_s} \:.\: f_s\)
Pedoman menentukan tanda (+) dan (−)
Apabila pendengar/sumber mendekat, maka frekuensi pendengar akan bertambah besar.
Sebaliknya, apabila pendengar/sumber menjauh, maka frekuensi pendengar akan bertambah kecil.
D. Dawai/Senar
Cepat rambat gelombang bunyi pada dawai
\(v = \sqrt{\dfrac {F}{\mu}}\) dimana \(\mu = \dfrac mL\)
\(v = \sqrt{\dfrac {F}{\rho \:.\: A}}\)
Frekuensi nada dasar (\(f_o\))
\(f_o = \dfrac {v}{2L}\)
Perbandingan frekuensi nada harmonik
\(f_o : f_1 : f_2 : f_3 = 1 : 2 : 3 : 4\)
Nada dasar
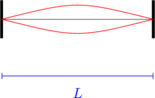
\(L = \frac 12 \lambda\)
\(\lambda = 2 L\)
Nada atas ke satu
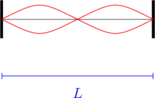
\(L = \lambda\)
Nada atas ke dua
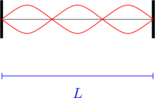
\(L = \frac 32 \lambda\)
\(\lambda = \frac 23 L\)
E. Pipa Organa
Pipa organa terbuka
\(f_o = \dfrac {v}{2L}\)
\(f_o : f_1 : f_2 = 1 : 2 : 3\)
Pipa organa tertutup
\(f_o = \dfrac {v}{4L}\)
\(f_o : f_1 : f_2 = 1 : 3 : 5\)
Gelombang stationer pada pipa organa terbuka
Nada dasar
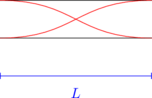
\(L = \frac 12 \lambda\)
\(\lambda = 2 L\)
Nada atas ke satu

\(L = \lambda\)
Nada atas ke dua

\(L = \frac 32 \lambda\)
\(\lambda = \frac 23 L\)
Gelombang stationer pada pipa organa tertutup
Nada dasar

\(L = \frac 14 \lambda\)
\(\lambda = 4 L\)
Nada atas ke satu

\(L = \frac 34 \lambda\)
\(\lambda = \frac 43 L\)
Nada atas ke dua

\(L = \frac 54 \lambda\)
\(\lambda = \frac 45 L\)
F. Layangan
\(f_L = | \: f_1 - f_2 \: |\)
G. Intensitas Dan Taraf Intensitas
Intensitas bunyi
\(I = \dfrac {P}{A}\) ... W/m²
P = daya sumber bunyi ... Watt
A = luas permukaan = 4 π R²
Perbandingan Intensitas bunyi
\(\dfrac {I_1}{I_2} = \left( \dfrac {R_2}{R_1} \right)^2\)
Taraf Intensitas bunyi
\(TI = 10 \:.\: \log \left (\dfrac {I}{I_o} \right)\) ... dB
Io = intensitas ambang bunyi = 10−12
Taraf Intensitas n buah sumber bunyi
\(TI_n = TI_1 +\log n \)
Taraf Intensitas pada jarak tertentu
\(TI_2 = TI_1 +\log \left( \dfrac {R_1}{R_2} \right)^2 \)
