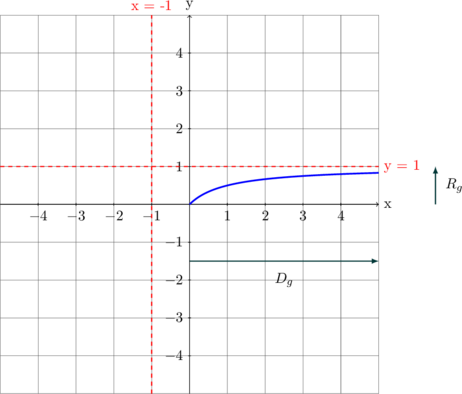
(i) Find the range of g
\(g : x \rightarrow \dfrac{x}{1 + x}, \: x \in R, \: x \geq 0\)
For \(x = 0, \: y = 0\)
For \(x \rightarrow + \sim, \: y \rightarrow 1\)
\(R_g : 0 \leq y < 1\)
\(g : x \rightarrow \dfrac{x}{1 + x}, \: - \sim \: < x < + \sim\)
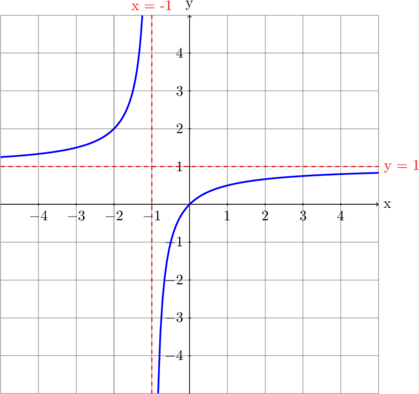
\(g : x \rightarrow \dfrac{x}{1 + x}, \: x \geq 0\)
(ii) Define the inverse function \(f^{-1}\) and the composite function \(gf\)
Given that \(f(x) = (x - 1)^2, \: x \geq 1\)
\begin{equation*}
\begin{split}
y & = (x - 1)^2 \\\\
x - 1 & = \pm \sqrt{y} \\\\
x & = 1 \pm \sqrt{y}
\end{split}
\end{equation*}
Since \(D_f: \: x \geq 1\), then \(x = 1 + \sqrt{y}\) for \(y \geq 0\)
\(f^{-1} (x) = 1 + \sqrt{x}, \: x \geq 0\)
(iii) Define the composite function \(gf\)
Substitute \(f\) into \(g\)
\begin{equation*}
\begin{split}
gf & = g \left[(x - 1)^2 \right] \\\\
gf & = \frac{(x - 1)^2}{1 + (x - 1)^2}
\end{split}
\end{equation*}
\(gf : x \rightarrow \dfrac{(x - 1)^2}{1 + (x - 1)^2}, \: x \: \in \: R, \: x \geq 1\)
Note:
Domain of \(gf\) is same with domain of \(f\)



