Tangent and Normal
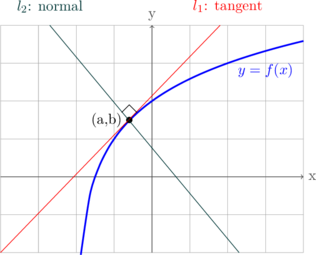
Tangent
Equation of tangent to the curve \(y = f(x)\) at \((a, b)\) can be determined by:
(1) Gradient of tangent
\(m = y' = f'(a)\)
(2) Equation of tangent
\(y - y_1= m \:.\: (x - x_1)\)
Normal
Normal is perpendicular line to the tangent at the same point.
Equation of normal to the curve \(y = f(x)\) at \((a, b)\) can be determined by:
(1) Gradient of tangent
\(m = y' = f'(a)\)
(2) Gradient of normal
\(m_t \:.\: m_n = -1\)
(2) Equation of normal
\(y - y_1= m_n \:.\: (x - x_1)\)
Example 01
Determine equation of tangent and normal to the curve \(f(x)= x^{3} + 4x^{2} - 5x + 1\) at \((1,2)\).
Tangent
Gradient of tangent at (1,2)
\begin{equation*} \begin{split} & f(x) = x^{3} + 4x^{2} - 5x + 1 \\\\ & f' (x) = 3x^{2} + 8x - 5 \\\\ & f'(1) = 3(1)^{2} + 8(1) - 5 \\\\ & m_t = 6 \end{split} \end{equation*}
Equation of tangent at (1,2)
\begin{equation*} \begin{split} & y - y_{1} = m_t \:.\: (x - x_1)\\\\ & y - 2 = 6 \:.\: (x - 1)\\\\ & y - 2 = 6x - 6\\\\ & \bbox[5px, border: 2px solid magenta] {y = 6x - 4} \end{split} \end{equation*}
Normal
Gradient of normal at (1,2)
\begin{equation*} \begin{split} & m_t \times m_n = -1 \\\\ & 6 \times m_n = -1 \\\\ & m_n = -\frac{1}{6} \end{split} \end{equation*}
Persamaan garis normal di titik (1,2)
\begin{equation*} \begin{split} & y - y_{1} = m_n \:.\: (x - x_1)\\\\ & y - 2 = -\frac{1}{6} \:.\: (x - 1)\\\\ & y - 2 = -\frac{1}{6} x + \frac{1}{6} \\\\ & \bbox[5px, border: 2px solid magenta] {y = -\frac{1}{6} x + 2\frac{1}{6}} \end{split} \end{equation*}
Exercise
