Differentiation

Nature of stationary point

\begin{equation*} \begin{split} f''(x) & > 0 \quad \text{local minimum} \\\\ f''(x) & < 0 \quad \text{local maximum} \end{split} \end{equation*}

Decreasing function

\(f' (x)<0\)

Curve sketching

• Determine curve intercept with axis
• Determine stationary points (if exists)
• Determine nature of stationary points (if exists)

Example

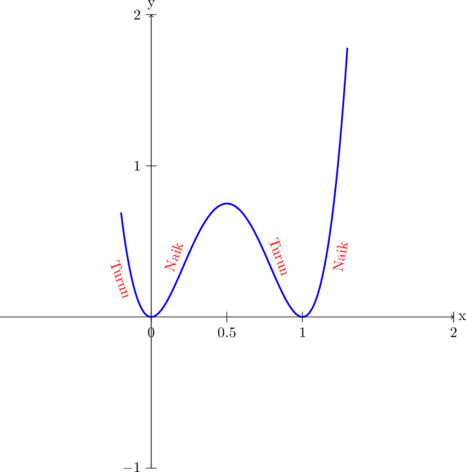
Given a function \(f(x) = x^4 - 2 x^3 + x^2\)

A. Determine its stationary points and its nature

B. Find the inverval where the function is increasing and decreasing

C. Sketch the curve

A. Stationary points

\begin{equation*} \begin{split} & f' (x) = 0 \\\\ & 4 x^{3} - 6 x^{2} + 2 x = 0 \\\\ & 2 x \:.\: (2x^{2} - 3x + 1) = 0\\\\ & 2x \:.\: (2x - 1)(x - 1) = 0\\\\ & x = 0 \text{ or } x = \frac{1}{2} \text{ or } x = 1 \end{split} \end{equation*}

Nature of stationary points

\begin{equation*} \begin{split} & f'' (x) = 12 x^{2} - 12 x + 2 \\\\ & f'' (0) = 2 \quad {\color {blue} \text{(local minimum)}} \\\\ & f'' (\frac 12) = -1 \quad {\color {blue} \text{(local maximum)}} \\\\ & f'' (1) = 2 \quad {\color {blue} \text{(local minimum)}} \end{split} \end{equation*}

Coordinate of stationary points

\begin{equation*} \begin{split} & f(x) = x^4 - 2 x^3 + x^2 \\\\ & f(0) = 0 \\\\ & f \left(\frac 12 \right) = \frac {1}{16} \\\\ & f(1) = 0 \end{split} \end{equation*}

Coordinate of stationary points are:

\((0,0)\) as local minimum

\(\left(\dfrac 12,\dfrac {1}{16} \right)\) as local maximum

\((1,0)\) as local minimum

B. Increasing and decreasing interval

Increasing function at the interval \(0 < x < \frac 12 \) dan \(x > 1\)

Decreasing function at the interval \(x < 0\) dan \(\frac 12 < x < 1\)

C. Curve sketching