Dasar-dasar Vektor
A. NOTASI VEKTOR
Vektor merupakan simbol untuk menyatakan suatu besaran yang memiliki nilai dan arah.
Misalnya vektor \(\overrightarrow a\) yang memiliki komponen 3 unit ke arah kanan dan 2 unit ke arah atas dapat dinyatakan sebagai berikut:
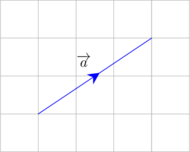
\(\overrightarrow{a} = \left( \begin{matrix} 3 \\ 2 \\ \end{matrix} \right) \)
\(\overrightarrow{a} = 3 \: \widehat i + 2 \: \widehat j \)
Suatu titik P dengan koordinat (a,b) memiliki vektor posisi \(\overrightarrow p = \left( \begin{matrix} a \\ b \\ \end{matrix} \right) \)
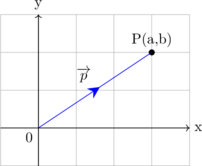
\(\overrightarrow{p} = \left( \begin{matrix} a \\ b \\ \end{matrix} \right) \)
\(\overrightarrow{p} = a \: \widehat i + b \: \widehat j \)
B. KESAMAAN DUA VEKTOR
Jika dua buah vektor \(\overrightarrow p = \left( \begin{matrix} a \\ b \\ \end{matrix} \right)\) dan \(\overrightarrow q = \left( \begin{matrix} c \\ d \\ \end{matrix} \right)\).
Jika \(\overrightarrow p = \overrightarrow q\), maka:
\(a = c \)
\(b = d \)
C. VEKTOR PERPINDAHAN
Suatu vektor yang menghubungkan dua titik P (a,b) dan Q (c,d) dapat dinyatakan dengan \(\overrightarrow {PQ} \)
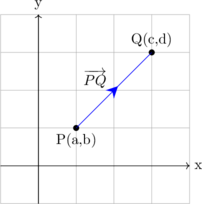
\begin{equation*} \begin{split} \overrightarrow{PQ} & = \overrightarrow q - \overrightarrow p \\\\ \overrightarrow{PQ} & = \left( \begin{matrix} c \\ d \\ \end{matrix} \right) - \left( \begin{matrix} a \\ b \\ \end{matrix} \right)\\\\ \overrightarrow{PQ} & = \left( \begin{matrix} c - a \\ d - b \\ \end{matrix} \right) \end{split} \end{equation*}
D. Panjang Dan Arah Vektor
Jika vektor \(\overrightarrow p = \left( \begin{matrix} a \\ b \\ \end{matrix} \right)\), maka:
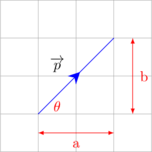
Panjang vektor
\(| \: \overrightarrow p \: |= \sqrt{a^2 + b^2} \)
Arah vektor
\(\tan \theta = \dfrac ba \)
E. Vektor Satuan
Sebuah vektor \(\overrightarrow p\) dinyatakan dengan \(\overrightarrow p = \left( \begin{matrix} a \\ b \\ \end{matrix} \right)\).
Maka vektor satuan dari \(\overrightarrow p\) adalah vektor yang memiliki arah sama dengan vektor \(\overrightarrow p\) namun memiliki panjang 1 satuan.
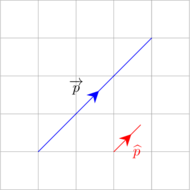
Vektor satuan dari \(\overrightarrow p\) dilambangkan dengan \(\widehat p\)
\(\widehat p = \dfrac {\overrightarrow p}{| \: \overrightarrow p \: |}\)
\(\widehat p = \dfrac {\left( \begin{matrix} a \\ b \\ \end{matrix} \right)}{\sqrt{a^2 + b^2}} \)
F. Perkalian Skalar Pada Vektor
Diketahui vektor \(\overrightarrow p = \left( \begin{matrix} a \\ b \\ \end{matrix} \right)\) dan skalar \(k\)
\(k \:.\: \overrightarrow p = k \:.\: \left( \begin{matrix} a \\ b \\ \end{matrix} \right) = \left( \begin{matrix} k \:.\: a \\ k \:.\: b \\ \end{matrix} \right)\)
G, Penjumlahan Dan Pengurangan Vektor
Diketahui dua buah vektor \(\overrightarrow p = \left( \begin{matrix} a \\ b \\ \end{matrix} \right)\) dan \(\overrightarrow q = \left( \begin{matrix} c \\ d \\ \end{matrix} \right)\)
\(\overrightarrow p + \overrightarrow q = \left( \begin{matrix} a \\ b \\ \end{matrix} \right) + \left( \begin{matrix} c \\ d \\ \end{matrix} \right) = \left( \begin{matrix} a + c \\ b + d \\ \end{matrix} \right)\)
\(\overrightarrow p - \overrightarrow q = \left( \begin{matrix} a \\ b \\ \end{matrix} \right) - \left( \begin{matrix} c \\ d \\ \end{matrix} \right) = \left( \begin{matrix} a - c \\ b - d \\ \end{matrix} \right)\)
H. Dua Vektor Segaris (Collinear)
Dua vektor \(\overrightarrow p\) dan \(\overrightarrow q\) yang segaris/collinear (terletak pada garis yang sama) akan memenuhi:
\(\overrightarrow p = k \:.\: \overrightarrow q\)
k adalah konstanta.
I. Tiga Vektor Sebidang (Coplanar)
Tiga vektor \(\overrightarrow p\), \(\overrightarrow q\) dan \(\overrightarrow r\) yang sebidang/coplanar (terletak pada bidang yang sama) akan memenuhi:
\(\overrightarrow r = m \:.\: \overrightarrow p + n \:.\: \overrightarrow q\)
m dan n adalah konstanta.
SOAL LATIHAN
