Metode Komponen Vektor
Sebuah vektor dapat diurai menjadi dua vektor (komponen arah x dan komponen arah y)
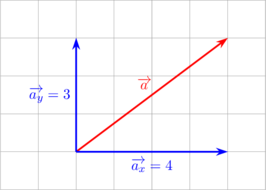
\(\overrightarrow a_x = 4\) dan \(\overrightarrow a_y = 3\)
\(\overrightarrow a = 4 \: \overrightarrow i + 3 \: \overrightarrow j\)
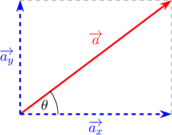
\(\cos \theta = \dfrac {\overrightarrow {a_x}}{a} \rightarrow \overrightarrow {a_x} = \overrightarrow a \:.\: \cos \theta\)
\(\sin \theta = \dfrac {\overrightarrow {a_y}}{a} \rightarrow \overrightarrow {a_y} = \overrightarrow a \:.\: \sin \theta\)
Menentukan resultan dengan metode komponen vektor
Tentukan resultan dari tiga buah vektor di bawah ini:
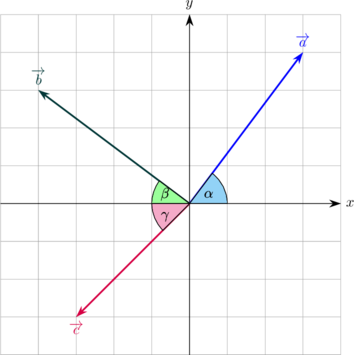
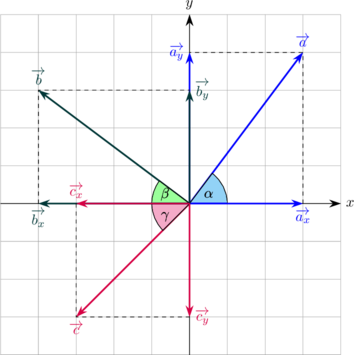
| Vektor | Komponen arah X | Komponen arah Y |
| \(\overrightarrow a\) | \(\overrightarrow a_x = a \cos \alpha\) | \(\overrightarrow a_y = a \sin \alpha\) |
| \(\overrightarrow b\) | \(\overrightarrow b_x = -b \cos \beta\) | \(\overrightarrow b_y = b \sin \beta\) |
| \(\overrightarrow c\) | \(\overrightarrow c_x = -c \cos \gamma\) | \(\overrightarrow c_y = -c \sin \gamma\) |
| \(\Sigma \overrightarrow X = \overrightarrow a_x + \overrightarrow b_x + \overrightarrow c_x\) | \(\Sigma \overrightarrow Y = \overrightarrow a_y + \overrightarrow b_y + \overrightarrow c_y\) |
\(|R| = \sqrt{(\Sigma \overrightarrow X)^2 + (\Sigma \overrightarrow Y)^2} \quad \tan \theta = \dfrac{\Sigma \overrightarrow Y}{\Sigma \overrightarrow X} \)
Catatan:
(tanda − ditambahkan pada komponen \(\overrightarrow b_x, \: \overrightarrow c_x\) dan \(\overrightarrow c_y\) karena ke arah x negatif dan y negatif.
SOAL LATIHAN
