I. PART 1
QUESTION 01
\(\log_5 0.008 = \bbox[10px, border: 2px solid red]{(1)}\), \(\left( \sqrt[6] {16} \right)^3 = \bbox[10px, border: 2px solid red]{(2)}\)
QUESTION 02
\(\sin 75^{\text{o}} + \sin 120^{\text{o}} - \cos 150^{\text{o}} + \cos 165^{\text{o}} = \bbox[10px, border: 2px solid red]{(1)}\).
QUESTION 03
\(\dfrac {1}{3 \:.\: 6} + \dfrac {1}{6 \:.\: 9} + \dfrac {1}{9 \:.\: 12} + \dfrac {1}{12 \:.\: 15} = \bbox[10px, border: 2px solid red]{(1)}\)
QUESTION 04
The number of integers that satisfy the following inequalities \(-x < x^2 < 6\) is \(\bbox[10px, border: 2px solid red]{(1)}\)
QUESTION 05
Among four-digit integers where digits are all different numerals, the total possible number of integers that are greater than or equal to 5000 is \(\bbox[10px, border: 2px solid red]{(1)}\).
QUESTION 06
When \(\vec a + \vec b + \vec c = 0\) and \(\| \vec a \| = \| \vec b \| = \| \vec c \| = 1\), ,then the degree measure of the angle between \(\vec a\) and \(\vec b\) is \(\bbox[10px, border: 2px solid red]{(1)}\) and \(\| \vec a - \vec b \| = \bbox[10px, border: 2px solid red]{(2)}\).
QUESTION 07
In the progression \(3, 4, 6, 10, 18, \dotso\), the numeral of the 8th term is \(\bbox[10px, border: 2px solid red]{(1)}\), and the number of term that is 1026 is \(\bbox[10px, border: 2px solid red]{(2)}\).
QUESTION 08
Let \(f(x) = x^2 - 4x + 1\).
(i) \(f(-2) = \bbox[10px, border: 2px solid red]{(1)}\)
(ii) If \(f(x) = 0, x = \bbox[10px, border: 2px solid red]{(2)} \text{ or } x = \bbox[10px, border: 2px solid red]{(3)}\) , where \((2) < (3)\)
(iii) The area bounded by the parabola \(y = f(x)\) and the x-axis is \(\bbox[10px, border: 2px solid red]{(4)}\)
QUESTION 09
In a space with a coordinate system, there are three points \(A(0,1,1), B(-1,-1,2)\) and \(C(2,3,1)\). The area of \(\Delta ABC\) is \( \bbox[10px, border: 2px solid red]{(1)}\).
II. PART 2
A quadrangle ABCD which is inscribed in a circle on a plane satisfies 2AB=AC, BC=3, BD = DC and ∠BAC=60º.
QUESTION 01
(i) The radius of the circumscribed circle of the quadrangle ABCD is \(\bbox[10px, border: 2px solid red]{(1)}\)
(ii) \(AC = \bbox[10px, border: 2px solid red]{(2)}\)
(iii) \(\angle BDC = \bbox[10px, border: 2px solid red]{(3)}\)
(iv) The area of \(\Delta BDC = \bbox[10px, border: 2px solid red]{(4)}\)
(v) The scalar product of two vectors \(\overrightarrow {DC} \cdot \overrightarrow {CA} = \bbox[10px, border: 2px solid red]{(5)}\)
III PART 3
QUESTION 01
On the plane \(xy\), the graph of the parabola \(y = ax^2 + bx + c\) is shown in the figure below. Judge whether the following expressions are larger than or smaller than zero.
Fill in the blanks with the correct marks: > or < .
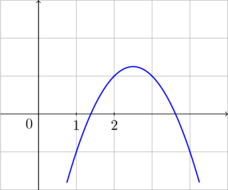
(1) \(a \: \bbox[10px, border: 2px solid red]{(1)} \: 0\)
(2) \(4ac-b^2 \: \bbox[10px, border: 2px solid red]{(2)} \: 0\)
(3) \(a + b + c \: \bbox[10px, border: 2px solid red]{(3)} \: 0\)
(4) \(4a - 2b + c \: \bbox[10px, border: 2px solid red]{(4)} \: 0\)
(5) \(\dfrac ca \: \bbox[10px, border: 2px solid red]{(5)} \: 0\)
(6) \(\dfrac ba \: \bbox[10px, border: 2px solid red]{(6)} \: 0\)
(7) \(b + 4a \: \bbox[10px, border: 2px solid red]{(7)} \: 0\)
(8) \(2a + b \: \bbox[10px, border: 2px solid red]{(8)} \: 0\)
