A. GARIS SINGGUNG DAN GARIS NORMAL

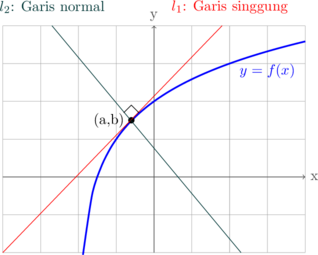
Gradien garis singgung pada kurva \(y = f(x)\) di titik \((a, b)\):

\(m = y' = f'(a)\)

Garis Normal

Garis normal adalah garis yang tegak lurus garis singgung pada titik yang sama. Gradien garis normal:

\(m_s \:.\: m_n = -1\)

B. TITIK STATIONER

Titik stationer

\begin{equation*} f'(x) = 0 \end{equation*}

Jenis titik stationer

\begin{equation*} \begin{split} f''(x) & > 0 \quad \text{titik minimum lokal} \\\\ f''(x) & < 0 \quad \text{titik maksimum lokal} \\\\ f''(x) & = 0 \quad \text{titik belok} \end{split} \end{equation*}

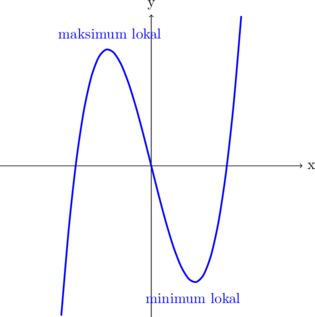
Fungsi naik dan Fungsi Turun

Interval fungsi naik dan fungsi turun dapat ditentukan dengan cara:

Fungsi naik → \(f' (x)>0\)

Fungsi turun → \(f' (x)<0\)

C. MAKSIMUM DAN MINIMUM

Langkah-langkah menyelesaikan soal aplikasi maksimum dan minimum:

(1)   bentuk persamaan dengan hanya mengandung satu variabel saja

(2)   bila persamaan mengandung dua variabel, cari dahulu hubungan antara dua variabel

(3)   gunakan turunan pertama untuk menentukan nilai stationer \((f' = 0)\)

(4)   gunakan turunan kedua untuk menentukan jenis stationer (maksimum atau minimum)

D. LAJU PERUBAHAN

Pemecahan masalah yang berkaitan dengan laju perubahan menggunakan aturan rantai:

\(\dfrac {dy}{dt} = \dfrac {dy}{dx} \times \dfrac {dx}{dt}\)

E. PERKIRAAN

Metode perkiraan/pendekatan untuk perubahan yang kecil:

\(\dfrac {dy}{dx} = \dfrac {\Delta y}{\Delta x}\)

F. KECEPATAN DAN PERCEPATAN

Jika \(s = f(t)\) menyatakan fungsi posisi sebuah benda yang bergerak dalam waktu t detik, maka:

\(s = f(t)\)

\(v = s' = f'(t)\)

\(a = v' =f''(t)\)