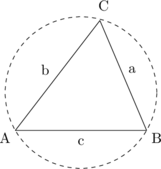
\(\bbox[10px, border: 2px solid red]{ \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R}\)

\(R\) adalah jari-jari lingkaran luar segitiga

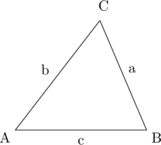
\(\bbox[10px, border: 2px solid red]{a^2 = b^2 + c^2 - 2 \:.\: b \:.\: c \:.\: \cos A}\)

Bentuk lain rumus di atas adalah:

\(\bbox[10px, border: 2px solid red]{\cos A = \dfrac {b^2 + c^2 - a^2}{2 \:.\: b \:.\: c}}\)

\(\bbox[10px, border: 2px solid red]{L = \dfrac 12 \:.\: a \:.\: b \:.\: \sin C}\)

\(\bbox[10px, border: 2px solid red]{L = \sqrt{s(s - a)(s - b)(s - c)}}\)

dimana \(s = \frac 12 (a + b + c)\)

Jari-jari lingkaran dalam adalah:

\(\bbox[10px, border: 2px solid red]{r = \dfrac {L}{s}}\)

Dimana \(s = \dfrac 12 (a + b + c)\)

Jari-jari lingkaran luar adalah:

\(\bbox[10px, border: 2px solid red]{R = \dfrac {a}{2 \:.\: \sin A} = \dfrac {a \:.\: b \:.\: c}{4 \:.\: L}}\)

Jari-jari lingkaran yang menyinggung sisi \(a\) adalah:

\(\bbox[10px, border: 2px solid red]{R_a = \dfrac {2L}{b + c - a}}\)