A. CEPAT RAMBAT BUNYI
Bunyi merupakan gelombang longitudinal, dimana arah rambat gelombang sejajar dengan arah getaran mediumnya. Bunyi juga termasuk gelombang mekanik, yang artinya bunyi hanya dapat merambat pada medium tertentu. Medium dapat berupa zat padat, cair atau gas.
Cepat rambat bunyi pada berbagai medium adalah:
Zat padat
\(\bbox[10px, border: 2px solid red]{v = \sqrt{\dfrac {E}{\rho}}}\)
Zat cair
\(\bbox[10px, border: 2px solid red]{v = \sqrt{\dfrac {B}{\rho}}}\)
Zat gas
\(\bbox[10px, border: 2px solid red]{v = \sqrt{\gamma \:.\: \dfrac {P}{\rho}} = \sqrt{\gamma \:.\: \dfrac {R \:.\: T}{M}}}\)
Secara umum, v (zat padat) > v (zat cair) > v (zat gas)
B. INTERFERENSI BUNYI
Konstruktif (kuat)
\(\bbox[10px, border: 2px solid red]{\Delta s = n \:.\: \lambda}\)
\(n = 0, 1, 2, 3, \dotso\)
Destruktif (lemah)
\(\bbox[10px, border: 2px solid red]{\Delta s = (n + \frac 12) \:.\: \lambda}\)
\(n = 0, 1, 2, 3, \dotso\)
C. EFEK DOPPLER
\(\bbox[10px, border: 2px solid red]{f_p = \dfrac {v \pm v_p}{v \pm v_s} \:.\: f_s}\)
Pedoman menentukan tanda (+) dan (−)
Apabila pendengar/sumber mendekat, maka frekuensi pendengar akan bertambah besar.
Sebaliknya, apabila pendengar/sumber menjauh, maka frekuensi pendengar akan bertambah kecil.
D. DAWAI/SENAR
Cepat rambat bunyi pada dawai
\(\bbox[10px, border: 2px solid red]{v = \sqrt{\dfrac {F}{\mu}} = \sqrt{\dfrac {F}{\rho \:.\: A}}}\) dimana \(\mu = \dfrac mL\)
Gelombang Stationer Pada Dawai
Frekuensi
\(f_o = \dfrac {v}{2L}\)
\(f_o : f_1 : f_2 = 1 : 2 : 3\)
Nada dasar
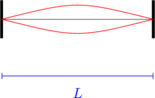
\(L = \dfrac 12 \lambda\)
Nada atas ke satu
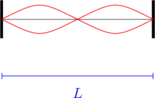
\(L = \lambda\)
Nada atas ke dua
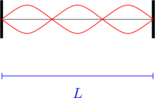
\(L = \dfrac 32 \lambda\)
E. PIPA ORGANA
1. Pipa organa terbuka
Gelombang stationer pada pipa organa terbuka
Frekuensi
\(f_o = \dfrac {v}{2L}\)
\(f_o : f_1 : f_2 = 1 : 2 : 3\)
Nada dasar
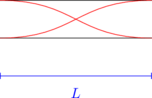
\(L = \dfrac 12 \lambda\)
Nada atas ke satu

\(L = \lambda\)
Nada atas ke dua

\(L = \dfrac 32 \lambda\)
2. Pipa organa tertutup
Gelombang stationer pada pipa organa tertutup
Frekuensi
\(f_o = \dfrac {v}{4L}\)
\(f_o : f_1 : f_2 = 1 : 3 : 5\)
Nada dasar

\(L = \dfrac 14 \lambda\)
Nada atas ke satu

\(L = \dfrac 34 \lambda\)
Nada atas ke dua

\(L = \dfrac 54 \lambda\)
F. LAYANGAN
Apabila kita mendengar dua bunyi dengan frekuensi yang berbeda sedikit, kita akan mendengar yang disebut layangan.
\(\bbox[10px, border: 2px solid red]{f_L = | \: f_1 - f_2 \: |}\)
G. INTENSITAS DAN TARAF INTENSITAS
1. Intensitas bunyi
\(\bbox[10px, border: 2px solid red]{I = \dfrac {P}{A}}\) ... W/m²
P = daya sumber bunyi ... Watt
A = luas bidang = \( 4 \pi R^2\)
Perbandingan Intensitas bunyi pada jarak berbeda
\(\bbox[10px, border: 2px solid red]{\dfrac {I_1}{I_2} = \left( \dfrac {R_2}{R_1} \right)^2}\)
2. Taraf Intensitas bunyi
\(\bbox[10px, border: 2px solid red]{TI = 10 \:.\: \log \left (\dfrac {I}{I_o} \right)}\) ... dB
\(I_o\) = intensitas ambang bunyi = \(10^{-12}\)
Taraf Intensitas dari n buah sumber bunyi yang identik
\(\bbox[10px, border: 2px solid red]{TI_n = TI_1 +\log n}\)
Taraf Intensitas pada jarak yang berbeda
\(\bbox[10px, border: 2px solid red]{TI_2 = TI_1 +\log \left( \dfrac {R_1}{R_2} \right)^2} \)
