A. TORSI/MOMEN GAYA
B. MOMEN INERSIA
A. Momen Inersia Benda Titik
Sebuah benda titik yang berotasi terhadap sumbu tertentu memiliki nilai momen inersia sistem yang besarnya:
\(I = m \:.\: R^2\)
m adalah massa benda
R adalah jarak benda ke pusat rotasi
Jika beberapa benda titik berotasi terhadap sumbu yang sama, nilai momen inersia sistem adalah:
\(I = \Sigma \: (m \:.\: R^2)\)
B. Momen Inersia Benda Tegar
Beberapa contoh momen inersia benda tegar dengan sumbu putar melalui pusat massa benda:
| No | Bentuk | Rumus |
|---|---|---|
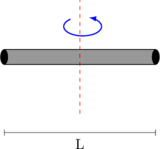
| 1 | Batang
|
\(I = \dfrac {1}{12} mL^2\) |
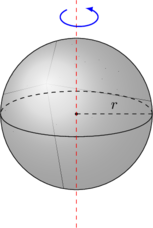
| 2 | Bola pejal
|
\(I = \dfrac 25 mR^2\) |
| 3 | Bola tipis berongga
|
\(I = \dfrac 23 mR^2\) |
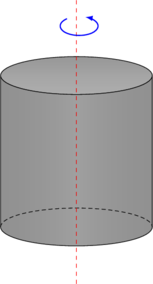
| 4 | Silinder pejal
|
\(I = \dfrac 12 mR^2\) |
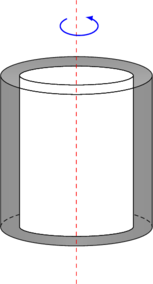
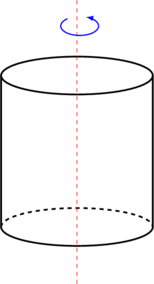
| 5 | Silinder berongga
|
\(I = \dfrac 12 m(R_1^2 + R_2^2)\) |
| 6 | Silinder tipis (cincin)
|
\(I = mR^2\) |
Teorema sumbu paralel
Momen inersia benda tegar bila sumbu rotasi digeser sejajar sejauh d:
\(I' = I + md^2\)
C. ROTASI BENDA TEGAR
D. HUKUM KEKEKALAN ENERGI
\begin{equation*} \begin{split} & EM_{(1)} = EM_{(2)} \\\\ & EP_{(1)} + EK_{(1)} = EP_{(2)} + EK_{(2)} \\\\ & EP_{(1)} + EK_{\text{translasi }(1)} + EK_{\text{rotasi }(1)} = EP_{(2)} + EK_{\text{translasi }(2)} + EK_{\text{rotasi }(2)} \\\\ & m \:.\: g \:.\: h_1 + \tfrac 12 \:.\: m \:.\: v_1^2 + \tfrac 12 \:.\: I \:.\: \omega_1^2 = m \:.\: g \:.\: h_2 + \tfrac 12 \:.\: m \:.\: v_2^2 + \tfrac 12 \:.\: I \:.\: \omega_2^2 \end{split} \end{equation*}
Perlu diingat juga:
Momen inersia
(1) silinder pejal = \(\tfrac 12 mR^2\)
(2) bola pejal = \(\tfrac 25 mR^2\)
Hubungan antara \(v\) dan \(\omega\)
\(v = \omega \:.\: R\)
E. MOMENTUM SUDUT
Benda yang melakukan rotasi memiliki momentum sudut (L) yang besarnya:
\(L = I \:.\: \omega\)
Bila tidak ada gaya luar yang bekerja, momentum sudut benda yang berotasi memiliki nilai konstan (tidak berubah), walaupun terjadi perubahan momen inersia (I) atau kecepatan sudutnya (ω).
\(L_1 = L_2\)
\(I_1 \:.\: \omega_1 = I_2 \:.\: \omega_2\)