A. MODULUS ELASTISITAS
1. Tegangan
Saat suatu benda padat diberi gaya tekan atau gaya tarik, benda akan mengalami tegangan atau stress. Tegangan atau stress didefinisikan sebagai gaya tekan/tarik per luas penampang.
\(\sigma = \dfrac{F}{A} \quad \dotso \text{ N/m}^2 \)
2. Regangan
Saat benda padat mengalami gaya tekan atau gaya tarik, benda dapat mengalami deformasi/perubahan panjang. Rasio antara perubahan panjang dan panjang mula-mula disebut dengan regangan atau strain.
\(\varepsilon = \dfrac{\Delta L}{L_o}\)
3. Modulus Elastisitas
Modulus elastisitas modulus young) suatu material adalah sifat fisik yang digunakan untuk mengukur kekuatan material. Semakin besar nilai modulus elastisitas suatu material, semakin kuat material tersebut untuk menahan beban tekan atau tarik.
Modulus elastisitas atau modulus young didefinisikan sebagai tegangan dibagi regangan.
\begin{equation*} \begin{split} & E = \frac{\sigma}{\varepsilon} \\\\ & E = \frac{\dfrac{F}{A}}{\dfrac{\Delta L}{L_o}} \\\\ & E = \frac{F \:.\: L_o}{A \:.\: \Delta L} \quad \dotso \text{ N/m}^2 \end{split} \end{equation*}
4. Konstanta Hooke Bahan (k)
\begin{equation*} \begin{split} & E = \frac{F \:.\: L_o}{A \:.\: \Delta L} \\\\ & F \:.\: L_o = E \:.\: A \:.\: \Delta L \\\\ & F = {\color {red} \frac{E \:.\: A}{L_o}} \:.\: \Delta L \\\\ & F = {\color {red} k} \:.\: \Delta L \\\\ & k = \dfrac{E \:.\: A}{L_o} \quad \dotso \text{ N/m} \end{split} \end{equation*}
5. Kurva Tegangan vs Regangan
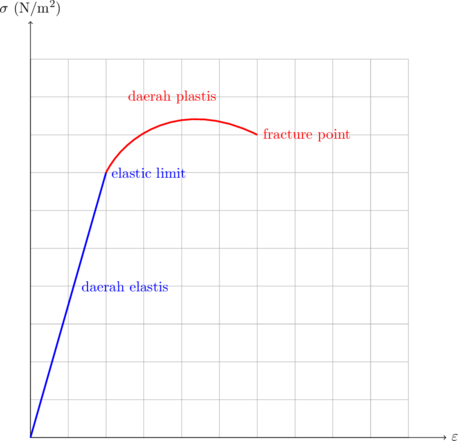
B. PEGAS
1. Gaya Pegas
Bila sebuah pegas diberi gaya tarik atau gaya tekan, pegas akan mengalami perubahan panjang. Besarnya perubahan panjang pegas dapat ditentukan dengan persamaan Hooke berikut:
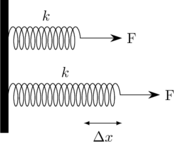
\(F = k \:.\: \Delta x \)
\(F\) : gaya tarik/gaya tekan pada pegas
\(k\) : konstanta pegas
\(\Delta x\) : perubahan panjang pegas
2. Energi Potensial Pegas
Saat pegas mengalami perubahan panjang, pegas mendapatkan energi yang disebut energi potensial pegas:
\( E_p = \frac{1}{2} \:.\: k \:.\: \Delta x^2 \quad \dotso \text{ Joule}\)
3. Grafik F vs \(\Delta x\)
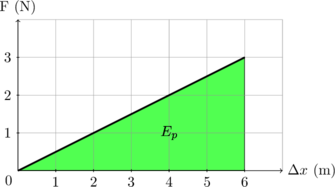
Luas daerah di bawah kurva (warna hijau) adalah besar energi potensial pada pegas
4. Susunan Pegas
Seri
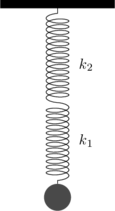
\(\dfrac{1}{k_T} = \dfrac{1}{k_1} + \dfrac{1}{k_2}\)
Paralel

\(k_T = k_1 + k_2\)
