A. DEBIT DAN KONTINUITAS
A. Sifat-sifat fluida ideal
(1) Aliran fluida tidak turbulen
Aliran fluida memiliki garis aliran (stream) yang sama
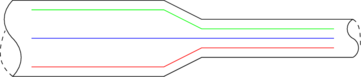
(2) Aliran fluida tunak (steady)
Kelajuan aliran fluida tidak tergantung pada waktu. Selama tidak ada perubahan penampang dan tekanan, kelajuan akan konstan.

(3) Tidak ada gesekan (non viscous)
Tidak ada gesekan di antara aliran dan antara aliran dengan dinding, fluida tidak kental
(4) Incompressible
Fluida tidak mengalami perubahan volume dan massa jenis saat mengalami perubahan tekanan
Dalam kenyataan, fluida ideal tidak ditemukan dalam kehidupan sehari-hari. Misalnya selalu ada gesekan antara aliran fluida dengan dinding.
Aliran fluida yang tenang dan berjalan pelan menyerupai kondisi fluida ideal.
Persamaan-persamaan dalam bab ini menggunakan asumsi bahwa fluida yang mengalir adalah fluida ideal.
Bagaimana dengan fluida yang tidak ideal? Harus dilihat kasus per kasus, misalnya aliran gas dalam pipa gas berbeda dengan aliran air dalam pipa air. Kamu dapat mempelajari materi ini secara khusus di Teknik Mesin dan Teknik Sipil tingkat universitas.
B. Debit
Debit adalah volume fluida yang mengalir setiap satuan waktu.
\(Q = \dfrac{V}{t} \quad \dotso \: m^3/s \)
\(Q\) = debit aliran
\(V\) = volume yang mengalir
\(t\) = waktu
\(Q = \dfrac{V}{t} = \dfrac{A \:.\: s}{t} = A \:.\: v\)
\(Q\) = debit aliran
\(A\) = luas penampang
\(v\) = kecepatan aliran
C. Persamaan Kontinuitas
Debit aliran fluida di setiap tempat selalu sama besar \((Q_1 = Q_2)\).
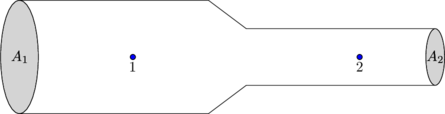
\(Q_1 = Q_2\)
\(A_1 \:.\: v_1 = A_2 \:.\: v_2\)
Perlu diingat:
\(A_1 \:.\: v_1 = A_2 \:.\: v_2\)
\(\dfrac {v_1}{v_2} = \dfrac {A_2}{A_1}\) → kecepatan aliran berbanding terbalik dengan luas penampang.
B. PERSAMAAN BERNOULLI
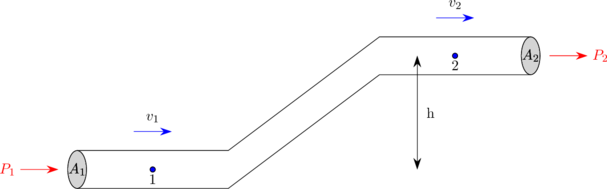
\(P_1 + \rho \: g \: h_1 + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \rho \: g \: h_2 + \frac{1}{2} \: \rho \: v_2^2\)
\(P + \rho \: g \: h + \frac{1}{2} \: \rho \: v^2 = \text{konstan} \)
A. Tangki air yang memiliki lubang kebocoran
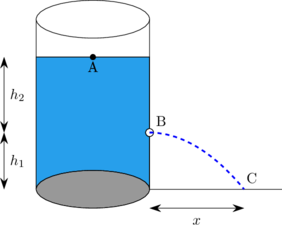
Rumus umum
\(v_B = \sqrt{2 \: g \: h_2}\)
\(x = 2 \sqrt{h_1 \:.\: h_2}\)
(tidak selalu bisa digunakan untuk tipe soal yang berbeda)
Gunakan penurunan rumus di bawah bila variasi berbeda
Persamaan Bernoulli
\(P_A + \rho \: g \: h_A + \frac{1}{2} \: \rho \: v_A^2 = P_B + \rho \: g \: h_B + \frac{1}{2} \: \rho \: v_B^2\)
\(P_A = P_B = \) tekanan udara
Laju penurunan air pada titik (A) pelan sehingga diasumsikan \(v_A = 0\)
\(\cancel {P_A} + \rho \: g \: h_A + 0 = \cancel {P_B} + \rho \: g \: h_B + \frac{1}{2} \: \rho \: v_B^2\)
\(\rho \: g \: h_A - \rho \: g \: h_B = \frac{1}{2} \: \rho \: v_B^2\)
\(\cancel {\rho} \: g \: (h_A - h_B) = \frac{1}{2} \: \cancel {\rho} \: v_B^2\)
\(g \: h_2 = \frac{1}{2} \: v_B^2\)
\(2 \: g \: h_2 = v_B^2\)
\(v_B = \sqrt {2 \: g \: h_2}\)
Gerak parabola
Gerak parabola dari B ke C
\(y = y_o + v_{oy} \:.\: t - \frac 12 \:.\: g \:.\: t^2\)
\(0 = h_B + 0 - \frac 12 \:.\: g \:.\: t^2\)
\(\frac 12 \:.\: g \:.\: t^2 = h_B\)
\(t = \sqrt{\dfrac {2h_1}{g}}\)
Jarak mendatar dari B ke C
\(x = v_x \:.\: t\)
\(x = \sqrt {2 \: g \: h_2} \:.\: \sqrt{\dfrac {2h_1}{g}}\)
\(x = \sqrt{2 \: g \: h_2 \:.\: \dfrac {2h_1}{g}}\)
\(x = 2 \sqrt {h_1 \:.\: h_2}\)
B. Gaya Angkat Pesawat
Bentuk muka sayap pesawat terbang didesain sedemikian rupa sehingga dapat mengarahkan arah angin ke arah atas atau ke arah bawah.
Jika pesawat ingin naik ke atas, maka lebih banyak angin yang bergerak ke atas. Sebaliknya, jika pesawat ingin bergerak turun, maka lebih banyak angin yang bergerak ke bawah.
PESAWAT BERGERAK KE ATAS
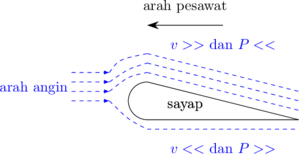
Sesuai dengan prinsip Bernoulli, \(P + \rho \: g \: h + \frac{1}{2} \: \rho \: v^2 = \text{konstan}\), dimana jika kecepatan membesar maka tekanan akan menurun. Sebaliknya jika kecepatan kecil, tekanan akan membesar.
Saat pesawat ingin bergerak ke atas, arah angin diarahkan ke atas sayap pesawat sehingga kecepatan angin di atas sayap lebih besar daripada kecepatan angin di bawah sayap. Maka tekanan di bawah sayap akan lebih besar daripada di atas sayap. Perbedaan tekanan ini yang akan membuat pesawat naik.
Penurunan Rumus
A bagian bawah sayap dan B bagian atas pesawat.
\(P_A + \rho \: g \: h_A + \frac{1}{2} \: \rho \: v_A^2 = P_B + \rho \: g \: h_B + \frac{1}{2} \: \rho \: v_B^2\)
Tebal sayap diabaikan sehingga perbedaan tinggi bagian bawah dan bagian atas sayap diabaikan.
\(P_A + \cancel {\rho \: g \: h_A} + \frac{1}{2} \: \rho \: v_A^2 = P_B + \cancel {\rho \: g \: h_B} + \frac{1}{2} \: \rho \: v_B^2\)
\(P_A + \frac{1}{2} \: \rho \: v_A^2 = P_B + \frac{1}{2} \: \rho \: v_B^2\)
\(P_A - P_B = \frac{1}{2} \: \rho \: v_B^2 - \frac{1}{2} \: \rho \: v_A^2\)
\(\Delta P = \frac{1}{2} \: \rho \: (v_B^2 - v_A^2)\)
Perbedaan tekanan antara \(P_A\) dan \(P_B\) menghasilkan gaya angkat pesawat.
\(\dfrac FA = \frac{1}{2} \: \rho \: (v_B^2 - v_A^2)\)
\(F = \frac{1}{2} \: \rho \: (v_B^2 - v_A^2) \: A\)
C. Siphon
Siphon merupakan sebuah sistem yang digunakan untuk memindahkan fluida dari tempat yang lebih tinggi ke tempat yang lebih rendah
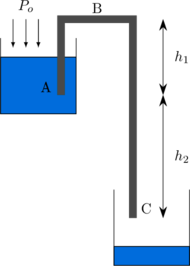
Air dipindahkan dari tangki yang lebih tinggi ke tangki yang lebih rendah dengan menggunakan pipa.
Pipa harus terisi penuh fluida sebelum digunakan.
Menentukan tinggi maksimum titik B
Tekanan di titik A sama dengan tekanan udara luar dan tekanan di B = 0
Kelajuan aliran di titik A ≈ 0
Beda tinggi antara titik A dan B adalah \(h_1\)
\begin{equation*} \begin{split} & P_A + \rho \: g \: h_A + \tfrac{1}{2} \: \rho \: v_A^2 = P_B + \rho \: g \: h_B + \tfrac{1}{2} \: \rho \: v_B^2 \\\\ & P_o + \rho \: g \: h_A + 0 = 0 + \rho \: g \: h_B + \tfrac{1}{2} \: \rho \: v_B^2 \\\\ & P_o - \tfrac{1}{2} \: \rho \: v_B^2 = \rho \: g \: (h_B - h_A) \\\\ & P_o - \tfrac{1}{2} \: \rho \: v_B^2 = \rho \: g \: h_1 \\\\ & h_1 = \frac {P_o}{\rho \: g} - \frac 12 v_B^2 \end{split} \end{equation*}
Tinggi maksimum titik B agar fluida tetap bisa mengalir → \(v_B = 0\)
\begin{equation*} \begin{split} & h_1 = \frac {P_o}{\rho \: g} \end{split} \end{equation*}
Menentukan kelajuan air di titik C
\begin{equation*} \begin{split} & P_A + \rho \: g \: h_A + \tfrac{1}{2} \: \rho \: v_A^2 = P_C + \rho \: g \: h_C + \tfrac{1}{2} \: \rho \: v_C^2 \\\\ & P_o + \rho \: g \: h_A + 0 = P_o + \rho \: g \: h_C + \tfrac{1}{2} \: \rho \: v_C^2 \\\\ & \cancel {\rho} \: g \: h_A - \rho \: g \: h_C = \tfrac{1}{2} \: \cancel {\rho} \: v_C^2 \\\\ & 2 \: g \: (h_A - h_C) = v_C^2 \\\\ & v_C = \sqrt{2 \: g \: h_2} \end{split} \end{equation*}
Kelajuan air di titik C didapat dari energi potensial air yang berada pada tangki atas.
C. ALAT UKUR KECEPATAN
A. Venturimeter terbuka
Venturimeter terbuka digunakan untuk mengukur kelajuan aliran zat cair.

\(A_1 > A_2 \rightarrow v_1 < v_2 \rightarrow P_1 > P_2\)
Permukaan cairan pada pipa (1) lebih tinggi daripada permukaan cairan pada pipa (2)
Persamaan Bernoulli
\begin{equation*} \begin{split} & P_1 + \cancel {\rho \: g \: h_1} + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \cancel {\rho \: g \: h_2} + \frac{1}{2} \: \rho \: v_2^2 \\\\ & {\color {blue} \text{Titik (1) dan (2) sejajar, maka } h_1 = h_2} \\\\ & P_1 - P_2 = \frac 12 \: \rho \: (v_2^2 - v_1^2) \quad {\color {red} \dotso (1)} \end{split} \end{equation*}
Manometer
\begin{equation*} \begin{split} & P_1 = \rho \:.\: g \:.\: h_A \\\\ & P_2 = \rho \:.\: g \:.\: h_B \\\\ & P_1 - P_2 = \rho \:.\: g \:.\: h_A - \rho \:.\: g \:.\: h_B \\\\ & P_1 - P_2 = \rho \:.\: g \:.\: (h_A - h_B) \\\\ & P_1 - P_2 = \rho \:.\: g \:.\: \Delta h \quad {\color {red} \dotso (2)} \end{split} \end{equation*}
Persamaan kontinuitas
\begin{equation*} \begin{split} & A_1 \:.\: v_1 = A_2 \:.\: v_2 \\\\ & v_2 = \frac {A_1}{A_2} \:.\: v_1 \quad {\color {red} \dotso (3)} \end{split} \end{equation*}
Substitusi persamaan (2) dan (3) ke persamaan (1)
\begin{equation*} \begin{split} & \rho \:.\: g \:.\: \Delta h = \frac 12 \:.\: \rho \:.\: \left[ \left(\frac {A_1}{A_2} \:.\: v_1\right)^2 - v_2^2 \right] \\\\ & \rho \:.\: g \:.\: \Delta h = \frac 12 \:.\: \rho \:.\: \left[ \left(\frac {A_1}{A_2}\right)^2 \:.\: v_1^2 - v_2^2 \right] \\\\ & \rho \:.\: g \:.\: \Delta h = \frac 12 \:.\: \rho \:.\: v_1^2 \:.\: \left[ \left(\frac {A_1}{A_2}\right)^2 - 1 \right] \\\\ & v_1^2 = \frac {\cancel {\rho} \:.\: g \:.\: \Delta h}{\frac 12 \:.\: \cancel {\rho} \left[ \left(\dfrac {A_1}{A_2}\right)^2 - 1 \right]} \\\\ & v_1^2 = \frac {2 \:.\: g \:.\: \Delta h}{\left[ \left(\dfrac {A_1}{A_2}\right)^2 - 1 \right]} \\\\ & \bbox[5px, border: 2px solid magenta]{v_1 = \sqrt{\frac {2 \:.\: g \:.\: \Delta h}{\left[ \left(\dfrac {A_1}{A_2}\right)^2 - 1 \right]}}} \end{split} \end{equation*}
B. Venturimeter tertutup
Venturimeter tertutup digunakan untuk mengukur kelajuan aliran air.
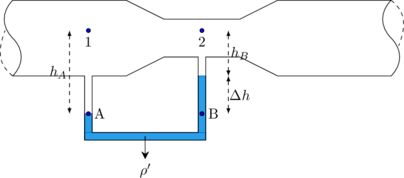
\(A_1 > A_2 \rightarrow v_1 < v_2 \rightarrow P_1 > P_2\)
Maka permukaan fluida pada pipa (1) lebih rendah daripada permukaan fluida pada pipa (2)
Persamaan Bernoulli
\begin{equation*} \begin{split} & P_1 + \cancel {\rho \: g \: h_1} + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \cancel {\rho \: g \: h_2} + \frac{1}{2} \: \rho \: v_2^2 \\\\ & {\color {blue} \text{Titik (1) dan (2) sejajar, maka } h_1 = h_2} \\\\ & P_1 - P_2 = \frac 12 \: \rho \: (v_2^2 - v_1^2) \quad {\color {red} \dotso (1)} \end{split} \end{equation*}
Manometer
\begin{equation*} \begin{split} & P_A = P_B \\\\ & P_1 + \rho \:.\: g \:.\: h_A = P_2 + \rho \:.\: g \:.\: h_B + \rho' \:.\: g \:.\: \Delta h \\\\ & P_1 - P_2 = \rho \:.\: g \:.\: h_B + \rho' \:.\: g \:.\: \Delta h - \rho \:.\: g \:.\: h_A \\\\ & P_1 - P_2 = \rho \:.\: g \:.\: (h_B - h_A) + \rho' \:.\: g \:.\: \Delta \\\\ & P_1 - P_2 = \rho \:.\: g \:.\: -\Delta h + \rho' \:.\: g \:.\: \Delta \\\\ & P_1 - P_2 = g \:.\: \Delta h \:.\: (\rho' - \rho) \quad {\color {red} \dotso (2)} \end{split} \end{equation*}
Persamaan kontinuitas
\begin{equation*} \begin{split} & A_1 \:.\: v_1 = A_2 \:.\: v_2 \\\\ & v_2 = \frac {A_1}{A_2} \:.\: v_1 \quad {\color {red} \dotso (3)} \end{split} \end{equation*}
Substitusi persamaan (2) dan (3) ke persamaan (1)
\begin{equation*} \begin{split} & g \:.\: \Delta h \:.\: (\rho' - \rho) = \frac 12 \: \rho \: (v_2^2 - v_1^2) \\\\ & g \:.\: \Delta h \:.\: (\rho' - \rho) = \frac 12 \:.\: \rho \:.\: \left[ \left(\frac {A_1}{A_2}\right)^2 \:.\: v_1^2 - v_2^2 \right] \\\\ & g \:.\: \Delta h \:.\: (\rho' - \rho) = \frac 12 \:.\: \rho \:.\: v_1^2 \:.\: \left[ \left(\frac {A_1}{A_2}\right)^2 - 1 \right] \\\\ & v_1^2 = \frac {g \:.\: \Delta h \:.\: (\rho' - \rho)}{\frac 12 \:.\: \rho \:.\: \left[ \left(\dfrac {A_1}{A_2}\right)^2 - 1 \right]} \\\\ & v_1^2 = \frac {2 \:.\: g \:.\: \Delta h \:.\: (\rho' - \rho)}{\rho \:.\: \left[ \left(\dfrac {A_1}{A_2}\right)^2 - 1 \right]} \\\\ & \bbox[5px, border: 2px solid magenta]{v_1 = \sqrt{\frac {2 \:.\: g \:.\: \Delta h \:.\: (\rho' - \rho)}{\rho \:.\: \left[ \left(\dfrac {A_1}{A_2}\right)^2 - 1 \right]}}} \end{split} \end{equation*}
C. Tabung Pitot
tabung pitot digunakan untuk mengukur kelajuan aliran gas
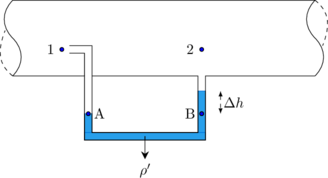
Pada tabung pitot, mulut pipa (1) diarahkan tegak lurus terhadap arah aliran gas (menjauhi pembaca), sehingga \(v_1 = 0\)
Persamaan Bernoulli
\begin{equation*} \begin{split} & P_1 + \cancel {\rho \: g \: h_1} + \frac{1}{2} \: \rho \: v_1^2 = P_2 + \cancel {\rho \: g \: h_2} + \frac{1}{2} \: \rho \: v_2^2 \\\\ & {\color {blue} \text{Titik (1) dan (2) sejajar, maka } h_1 = h_2 \text{ dan } v_1 = 0} \\\\ & P_1 - P_2 = \frac 12 \:.\: \rho \:.\: v_2^2 \quad {\color {red} \dotso (1)} \end{split} \end{equation*}
Manometer
\begin{equation*} \begin{split} & P_A = P_B \\\\ & P_1 = P_2 + \rho' \:.\: g \:.\: \Delta h \\\\ & P_1 - P_2 = \rho' \:.\: g \:.\: \Delta h \quad {\color {red} \dotso (2)} \end{split} \end{equation*}
Substitusi persamaan (2) ke persamaan (1)
\begin{equation*} \begin{split} & \rho' \:.\: g \:.\: \Delta h = \frac 12 \:.\: \rho \:.\: v_2^2 \\\\ & v_2^2 = \frac {\rho' \:.\: g \:.\: \Delta h}{\frac 12 \:.\: \rho} \\\\ & v_2^2 = \frac {2 \:.\: \rho' \:.\: g \:.\: \Delta h}{\rho} \\\\ & \bbox[5px, border: 2px solid magenta]{v_2 = \sqrt{\frac {2 \:.\: \rho' \:.\: g \:.\: \Delta h}{\rho}}} \end{split} \end{equation*}
