A. TEKANAN HIDROSTATIS
Tekanan adalah besarnya gaya per luas penampang.

\(P = \dfrac{F}{A} \quad \dotso \: \text{N/m}^2 \)
Tekanan Hidrostatis
Tekanan hidrostatis adalah tekanan akibat fluida (zat cair atau gas).
Misalnya tekanan akibat cairan di dalam sebuah tabung. Gaya berat cairan akan menekan dasar tabung.
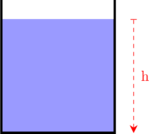
\(\bbox[5px, border: 2px solid red] {P_h = \rho_f \:.\: g \:.\: h \quad \dotso \: \text{Pa}}\)
\begin{equation*} \begin{split} P_h & = \frac{F}{A} \\\\ P_h & = \frac{m \:.\: g}{A} \\\\ P_h & = \frac{\rho_f \:.\: V \:.\: g}{A} \\\\ P_h & = \frac{\rho_f \:.\: A \:.\: h \:.\: g}{A} \\\\ P_h & = \frac{\rho_f \:.\: \cancel {A} \:.\: h \:.\: g}{\cancel {A}} \\\\ P_h & = \rho_f \:.\: g \:.\: h \end{split} \end{equation*}
\(P_h\) = tekanan hidrostatis
\(g\) = percepatan gravitasi
\(\rho_f\) = massa jenis fluida
\(h\) = kedalaman fluida diukur dari permukaan cairan
Tekanan Mutlak
Tekanan mutlak (tekanan total) pada dasar tabung adalah jumlah dari tekanan hidrostatis akibat cairan dan tekanan atmosfer.
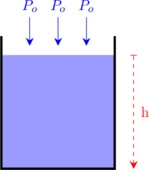
\(\bbox[5px, border: 2px solid red] {P = P_o + \rho_f \:.\: g \:.\: h}\)
\(P_o\) = tekanan atmosfer
Besar tekanan atmosfer pada permukaan laut adalah 1 atm atau \(10^5\) Pa
Tekanan Atmosfer
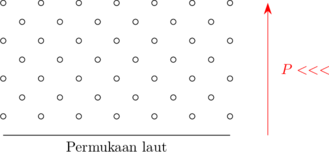
Tekanan atmosfer berasal dari berat partikel di udara (atmosfer). Tekanan atmosfer pada permukaan laut adalah 101.325 Pa, sering dibulatkan menjadi 100.000 Pa.
Semakin tinggi, tekanan atmosfer semakin berkurang.
Manometer
Manometer adalah sebuah pipa berbentuk U yang diisi oleh cairan tertentu. Manometer digunakan untuk mengukur tekanan gas. Manometer juga dapat digunakan untuk menentukan massa jenis cairan.
Ada 2 jenis manometer, yaitu manometer terbuka dan manometer tertutup.
MANOMETER TERBUKA

MANOMETER TERTUTUP

Prinsip dasar manometer, dua titik yang berada pada posisi sejajar memiliki tekanan yang sama.
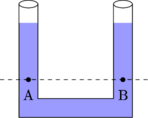
\(P_A = P_B\)
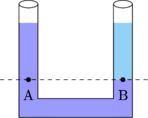
\(P_A = P_B\)
B. HUKUM PASCAL
Gaya yang dialami oleh zat cair dalam ruang tertutup akan diteruskan ke segala arah dan sama besar.
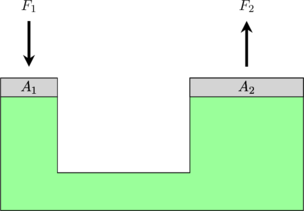
\begin{equation*} \begin{split} P_1 & = P_2 \\\\ \frac{F_1}{A_1} & = \frac{F_2}{A_2} \end{split} \end{equation*}
\(P_1\) dan \(P_2\) = tekanan pada titik 1 dan 2
\(F_1\) dan \(F_2\) = gaya tekan pada titik 1 dan 2
\(A_1\) dan \(A_2\) = luas penampang titik 1 dan 2
C. HUKUM ARCHIMEDES
Sebuah benda yang dicelupkan ke dalam suatu zat cair akan mengalami gaya ke atas.
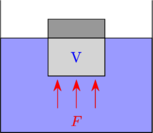
\(F_A = \rho_f \:.\: g \:.\: V_{\text{t}}\)
\(F_A\) = gaya ke atas atau gaya Archimedes
\(\rho_f\) = massa jenis fluida
\(g\) = percepatan gravitasi
\(V_t\) = volume benda di dalam fluida
D. TEGANGAN PERMUKAAN
Permukaan zat cair dapat diibaratkan seperti selaput tipis yang dapat menahan beban di atasnya. Besarnya beban yang dapat ditahan tergantung dari nilai tegangan permukaan.
\(\gamma = \dfrac{F}{2 \:.\: L} \quad \dotso \: \text{N/m}\)
\(\gamma\) = tegangan permukaan
\(L\) = panjang permukaan zat cair
Kapilaritas
Zat cair dalam pipa akan mengalami kenaikan/penurunan permukaan, tergantung dari sifat kohesi/adhesinya. Kohesi adalah gaya tarik-menarik molekul-molekul sejenis, dan adhesi adaah gaya tarik-menarik molekul-molekul berbeda jenis.
Bila sifat kohesi lebih besar daripada sifat adhesi, maka permukaan zat cair akan turun. Sebaliknya, bila sifat adhesi lebih besar daripada sifat kohesinya, permukaan zat cair akan naik.
Besar kenaikan atau penurunan permukaan zat cair adalah:
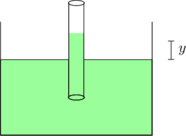
\(y = \dfrac{2 \:.\: \gamma \:.\: \cos \theta}{\rho_f \:.\: g \:.\: r}\)
\(y\) = kenaikan atau penurunan zat cair
\(\gamma\) = tegangan permukaan
\(\theta\) = sudut kontak
\(\rho_f\) = massa jenis zat cair
\(r\) = jari-jari wadah
E. GESEKAN DALAM FLUIDA
1. Gesekan Di Udara
Gesekan di udara, sering disebut drag force, bekerja dalam arah berlawanan dengan gerak benda. Besarnya drag force berbanding lurus dengan kuadrat kecepatan benda. Semakin besar kecepatan benda, semakin besar juga gaya hambatannya.
\(F \approx v^2\)
\(F = \dfrac 12 \:.\: C \:.\: A \:.\: \rho \:.\: v^2\)
\(F\) = gaya gesekan
\(C\) = koefisien gesekan
\(A\) = luas penampang
\(\rho\) = massa jenis udara
\(v\) = kecepatan benda
1. Gesekan Dalam Zat Cair
Gesekan dalam zat cair (viskositas zat cair) menghambat aliran cairan, dan menghambat gerakan benda apabila terdapat benda yang bergerak di dalam cairan tersebut. Besarnya viskositas berbanding lurus dengan kecepatan aliran/kecepatan benda.
\(F \approx v\)
Menurut hukum Stokes, besar gaya viskositas zat cair untuk benda berbentuk bola adalah:
\(F = 6 \pi \:.\: \eta \:.\: r \:.\: v\)
\(F\) = gaya gesekan
\(\eta\) = koefisien viskositas
\(r\) = jari-jari bola
\(v\) = kecepatan bola dalam fluida
Kecepatan terminal
Saat benda dijatuhkan ke dalam fluida, benda mengalami percepatan gravitasi sehingga kecepatannya meningkat. Saat kecepatan meningkat, gaya gesekan juga akan semakin besar. Gaya gesekan akan semakin besar sampai pada suatu waktu dimana percepatan benda nol, dan benda bergerak dengan kecepatan tetap (kecepatan terminal).
Dalam kasus hukum Stokes, kecepatan terminal dapat ditentukan dengan:
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & w - F_s = m \:.\: a \\\\ & m \:.\: g - 6 \pi \:.\: \eta \:.\: r \:.\: v = 0 \\\\ & 6 \pi \:.\: \eta \:.\: r \:.\: v = m \:.\: g \\\\ & 6 \pi \:.\: \eta \:.\: r \:.\: v = \rho_b \:.\: V \:.\: g \\\\ & 6 \pi \:.\: \eta \:.\: r \:.\: v = \rho_b \:.\: \frac 43 \pi \:.\: r^3 \:.\: g \\\\ & \bbox[5px, border: 2px solid red]{v = \frac {2 \:.\: \rho_b \:.\: r^2 \:.\: g}{9 \:.\: \eta}} \end{split} \end{equation*}
