A. GRAFIK FUNGSI EKSPONEN
Bentuk dasar grafik fungsi eksponen dapat dilihat pada contoh di bawah ini.
\(y = a^x, \: a > 1\)
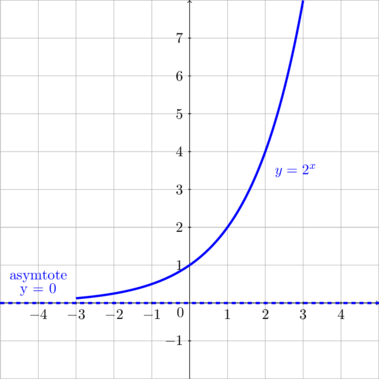
\(y = a^x, \: 0 < a < 1\)
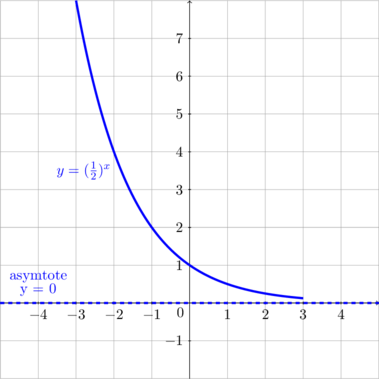
Transformasi Fungsi Eksponen
\(y = a^x \rightarrow y - k = a^{x - h}\)
Kurva bergeser ke atas sejauh \(k\) dan ke kanan sejauh \(h\).
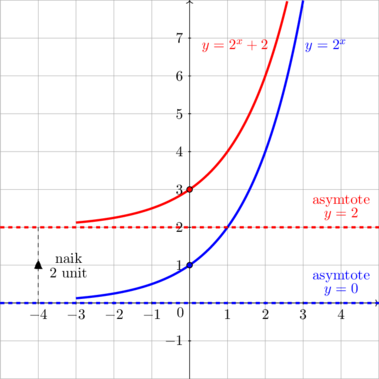
\(y = 2^x \rightarrow y - 2 = 2^x \)
Kurva bergeser ke atas 2 unit
Asymtote bergeser ke atas 2 unit
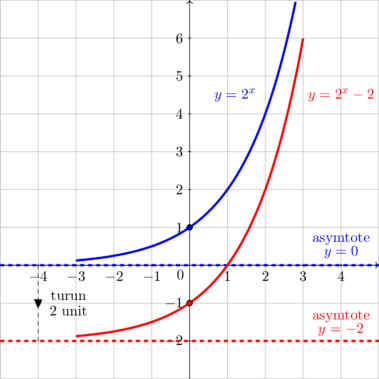
\(y = 2^x \rightarrow y + 2 = 2^x\)
Kurva bergeser ke bawah 2 unit
Asymtote bergeser ke bawah 2 unit
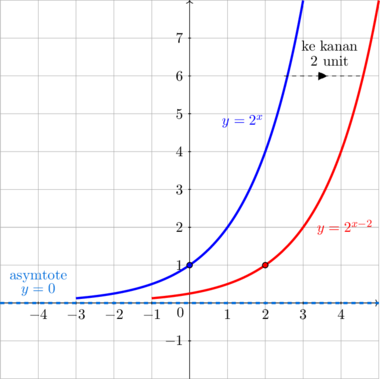
\(y = 2^x \rightarrow y = 2^{x - 2}\)
Kurva bergeser ke kanan 2 unit
Asymtote tidak berubah
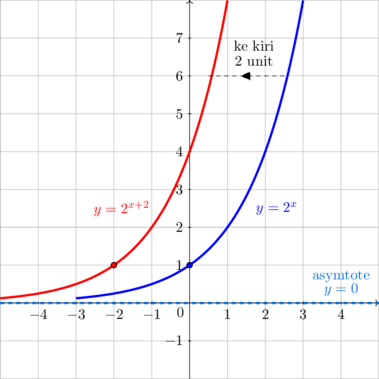
\(y = 2^x \rightarrow y = 2^{x + 2}\)
Kurva bergeser ke kiri 2 unit
Asymtote tidak berubah
Pertumbuhan dan Peluruhan
Pertumbuhan atau peluruhan dapat dinyatakan sebagai:
\(N = N_{\text{o}} \:.\: R^{\: t}\)
\(N_o\) = jumlah mula-mula
\(N\) = jumlah akhir
\(t\) = waktu
\(R\) = Laju pertumbuhan/peluruhan
Laju pertumbuhan: \(R > 1\)
Laju peluruhan: \(R < 1\)
B. PERSAMAAN EKSPONEN
Bentuk 1
\(\bbox[10px, border: 2px solid red]{a^{f(x)} = a^{g(x)}}\)
\( \cancel{a}^{f(x)} = \cancel{a}^{g(x)} \)
\( f(x) = g(x) \)
Bentuk 3
\(\bbox[10px, border: 2px solid red]{a^{f(x)} = b \: ^{g(x)}}\)
Menambahkan \(\log\) pada kedua ruas.
\( \log a^{f(x)} = \log b \: ^{g(x)}\)
\( f(x) \:.\: \log a = g(x) \:.\: \log b \)
Bentuk 5
\(\bbox[10px, border: 2px solid red]{f(x)^{h(x)} = g(x)^{h(x)}}\)
Solusi 1
\begin{equation*} \begin{split} & f(x)^{h(x)} = g(x)^{h(x)}\\\\ & f(x)^{\cancel{h(x)}} = g(x)^{\cancel{h(x)}}\\\\ & f(x) = g(x) \end{split} \end{equation*}
Solusi 2
\(h(x) = 0 \)
Dengan syarat nilai \(f(x) \neq 0\) dan \(g(x) \neq 0\)
Bentuk 6
\(\bbox[10px, border: 2px solid red]{h(x)^{f(x)} = h(x)^{g(x)}}\)
Solusi 1
\begin{equation*} \begin{split} & h(x)^{f(x)} = h(x)^{g(x)} \\\\ & \cancel {h(x)}^{f(x)} = \cancel {h(x)}^{g(x)} \\\\ & f(x) = g(x) \end{split} \end{equation*}
Solusi 2
\(h(x) = 1 \)
Solusi 3
\(h(x) = 0 \)
Dengan syarat nilai \(f(x) > 0\) dan \(g(x) > 0\)
Solusi 4
\(h(x) = -1 \)
Dengan syarat nilai \(f(x)\) dan \(g(x)\) keduanya bilangan ganjil atau keduanya bilangan genap
C. PERTIDAKSAMAAN EKSPONEN
Untuk a > 1
\begin{equation*} \begin{split} a^{f(x)} & > a^{g(x)} \\\\ \cancel {a}^{f(x)} & > \cancel {a}^{g(x)} \\\\ f(x) & > g(x) \end{split} \end{equation*}
Untuk a < 1
\begin{equation*} \begin{split} a^{f(x)} & > a^{g(x)} \\\\ \cancel {a}^{f(x)} & > \cancel {a}^{g(x)} \\\\ f(x) & < g(x) \quad {\color {red} \text{(tanda berubah)}} \end{split} \end{equation*}
