A. GRAFIK FUNGSI KUADRAT
1. Sketsa Grafik Fungsi Kuadrat
Grafik fungsi kuadrat \(y = ax^2 + bx + c\) dapat digambar dengan 2 cara:
A. Cara melengkapkan kuadrat
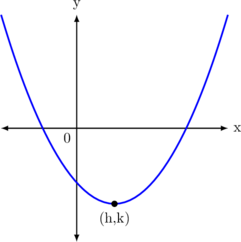
Titik puncak \((h,k)\) didapat dengan mengubah persamaan menjadi:
\(\bbox[10px, border: 2px solid red]{y = a(x - h)^2 + k}\)
B. Cara rumus
Titik puncak didapat dari rumus \(\bbox[10px, border: 2px solid red]{h = - \dfrac {b}{2a}}\)
Kemudian dengan mensubstitusikan \(h\) ke persamaan, akan didapat nilai \(k\).
Titik potong grafik dengan sumbu koordinat ditentukan dengan:
1. Titik potong dengan sumbu X → \(y = 0\)
2. Titik potong dengan sumbu Y → \(x = 0\)
2. Menentukan Persamaan Fungsi Kuadrat
Untuk menentukan persamaan fungsi kuadrat dari grafik, dapat dilakukan dengan:
A. Bila diketahui titik puncak \((h,k)\)
\(\bbox[10px, border: 2px solid red]{y = a(x - h)^2 + k}\)
B. Bila diketahui titik potong dengan sumbu X \((x_1,0)\) dan \((x_2,0)\)
\(\bbox[10px, border: 2px solid red]{y = a (x - x_1)(x - x_2)}\)
C. Bila diketahui tiga titik sembarang
Substitusi ketiga titik ke dalam persamaan \(y = ax^2 + bx + c\) dan lakukan metode eliminasi untuk menentukan nilai \(a\), \(b\) dan \(c\).
B. DOMAIN DAN RANGE
Domain adalah daerah asal dan Range adalah daerah hasil.
Pada grafik fungsi kuadrat, domain dinyatakan dalam variabel \(x\) dan range dinyatakan dalam variabel \(y\).
Kurva menghadap ke atas
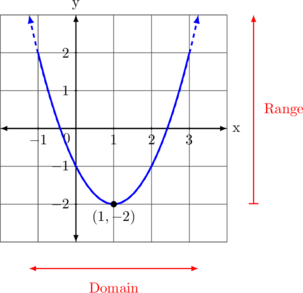
DOMAIN
Kurva dapat diperpanjang ke arah kiri dan kanan tak terbatas, maka dari itu nilai x tidak terbatas. Sehingga domain fungsi adalah \(x \: \in \: R\)
RANGE
Titik terendah kurva berada pada \(y = -2\) sedangkan titik tertingginya tidak terbatas. Oleh karena itu, range fungsi adalah \(y \geq -2\)
Kurva menghadap ke bawah
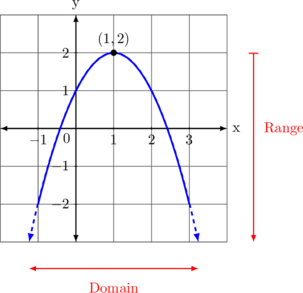
DOMAIN
Kurva dapat diperpanjang ke arah kiri dan kanan tak terbatas, maka dari itu nilai x yang terbatas. Sehingga domain fungsi adalah \(x \: \in \: R\)
RANGE
Titik tertinggi kurva berada pada \(y = 2\) sedangkan titik terendahnya tidak terbatas. Oleh karena itu, range fungsi adalah \(y \leq 2\)
