FUNGSI LOGARITMA
A. GRAFIK FUNGSI LOGARITMA
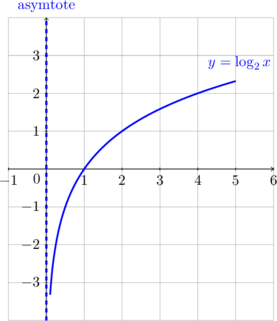
\(y = \log_2 x, \: a > 1\)
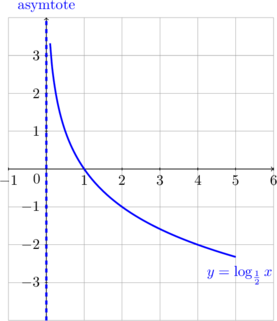
\(y = \log_{\frac 12} x, \: 0 < a < 1\)
B. PERSAMAAN LOGARITMA
Basis yang sama
\(^a \log f(x) = \: ^a \log g(x) \)
\(\cancel {^a \log} f(x) = \: \cancel {^a \log} g(x) \)
\(f(x) = g(x) \)
Syarat basis
\(a > 0\) dan \(a \neq 1\)
Syarat terdefinisi
\(f(x_1) > 0\) dan \(g(x_1) > 0\)
C. PERTIDAKSAMAAN LOGARITMA
Untuk \(a > 1\)
\begin{equation*} \begin{split} ^a \log f(x) & > \: ^a \log g(x) \\\\ \cancel {^a \log} f(x) & > \: \cancel {^a \log} g(x) \\\\ f(x) & > \: g(x) \end{split} \end{equation*}
Untuk \(0 < a < 1\)
\begin{equation*} \begin{split} ^a \log f(x) & > \: ^a \log g(x) \\\\ \cancel {^a \log} f(x) & > \: \cancel {^a \log} g(x) \\\\ f(x) & < \: g(x) \quad {\color {red} \text{(tanda berubah)}} \end{split} \end{equation*}
Untuk kedua bentuk di atas, harus memenuhi syarat terdefinisi.
\(f(x) > 0\) dan \(g(x) > 0\)
