A. GRAFIK FUNGSI TRIGONOMETRI
| Grafik | Keterangan |
|---|---|
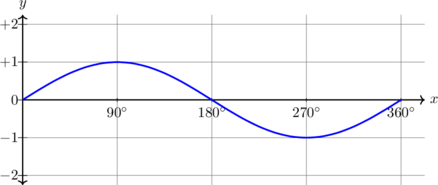
| \(y = \sin x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(360^\text{o}\)
Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
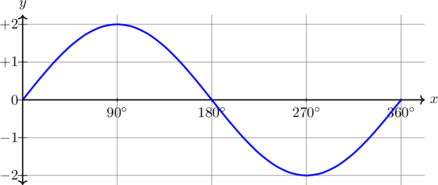
| \(y = 2 \sin x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperbesar 2 kali dalam arah Y
Periode = \(360^\text{o}\) Amplitudo = 2 \(y_{\text{max}} = 2\) \(y_{\text{min}} = -2\) |
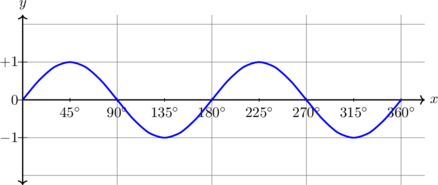
| \(y = \sin 2x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperkecil \(\dfrac 12\) kali dalam arah X
Periode = \(\dfrac {360^{\text{o}}}{2} = 180^{\text{o}}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
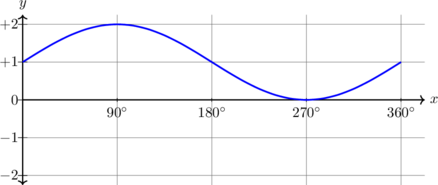
| \(y = \sin x + 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke atas
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 2\) \(y_{\text{min}} = 0\) |
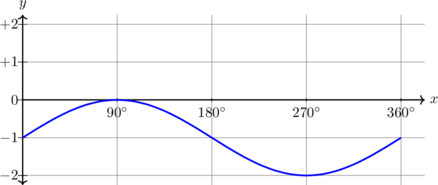
| \(y = \sin x - 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke bawah
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 0\) \(y_{\text{min}} = -2\) |
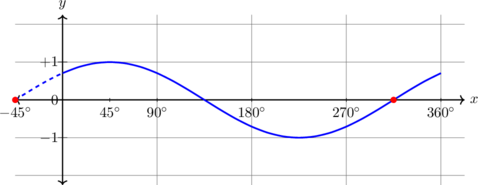
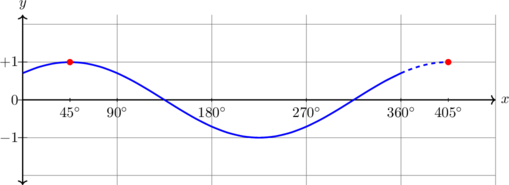
| \(y = \sin (x - 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kanan
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
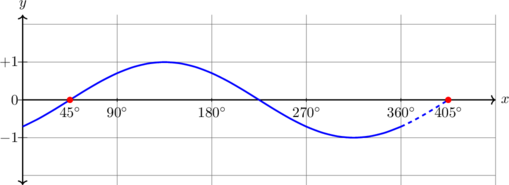
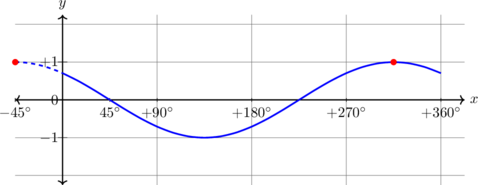
| \(y = \sin (x + 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kiri
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| Grafik | Keterangan |
|---|---|
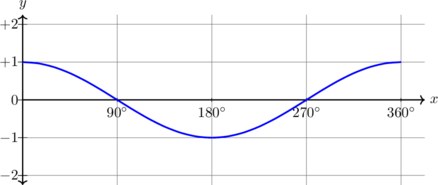
| \(y = \cos x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(360^\text{o}\)
Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
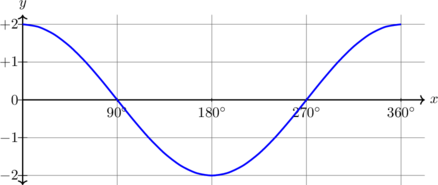
| \(y = 2 \cos x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperbesar 2 kali dalam arah Y
Periode = \(360^\text{o}\) Amplitudo = 2 \(y_{\text{max}} = 2\) \(y_{\text{min}} = -2\) |
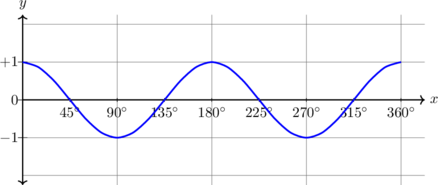
| \(y = \cos 2x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva diperkecil \(\dfrac 12\) kali dalam arah X
Periode = \(\dfrac {360^{\text{o}}}{2} = 180^{\text{o}}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
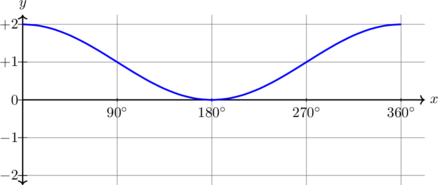
| \(y = \cos x + 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke atas
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 2\) \(y_{\text{min}} = 0\) |
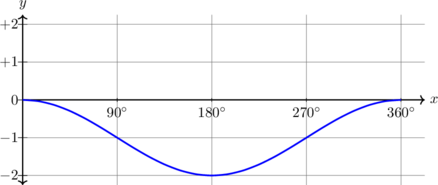
| \(y = \cos x - 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke bawah
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 0\) \(y_{\text{min}} = -2\) |
| \(y = \cos (x - 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kanan
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| \(y = \cos (x + 45^\text{o}) , \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kiri
Periode = \(360^\text{o}\) Amplitudo = 1 \(y_{\text{max}} = 1\) \(y_{\text{min}} = -1\) |
| Grafik | Keterangan |
|---|---|
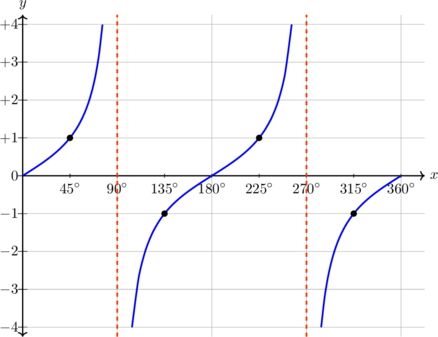
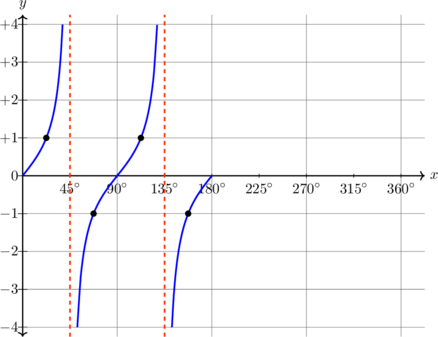
| \(y = \tan x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(180^\text{o}\)
Pada x = 45º, y = 1
|
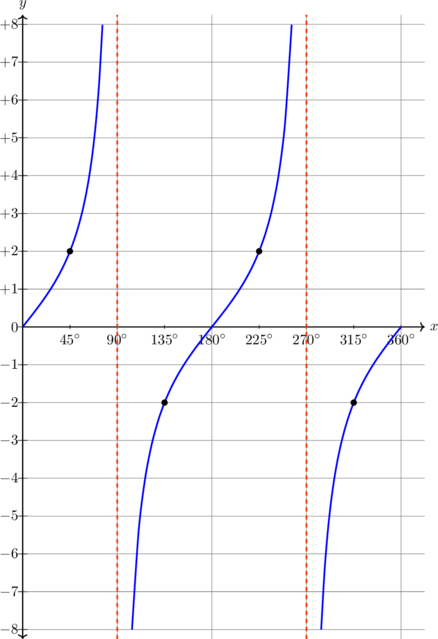
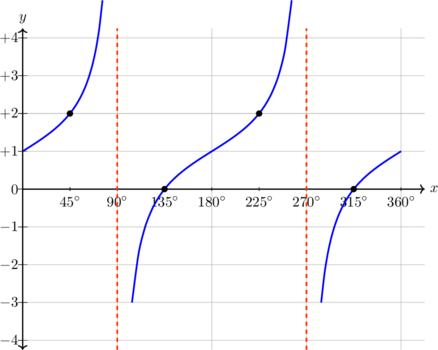
| \(y = 2 \tan x, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Periode = \(180^\text{o}\)
Pada x = 45º, y = 2 |
| \(y = \tan 2x, \quad 0^\text{o} \leq x \leq 180^\text{o}\)
|
Periode = \(\dfrac {180^{\text{o}}}{2} = 90^{\text{o}}\)
Pada x = 22.5º, y = 1 |
| \(y = \tan x + 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke atas
Periode = \(180^\text{o}\) Pada x = 45º, y = 2
|
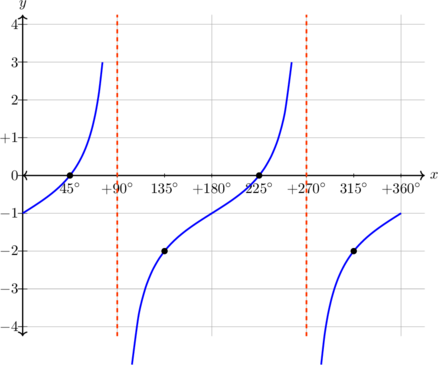
| \(y = \tan x - 1, \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 1 unit ke bawah
Periode = \(180^\text{o}\) Pada x = 45º, y = 0 |
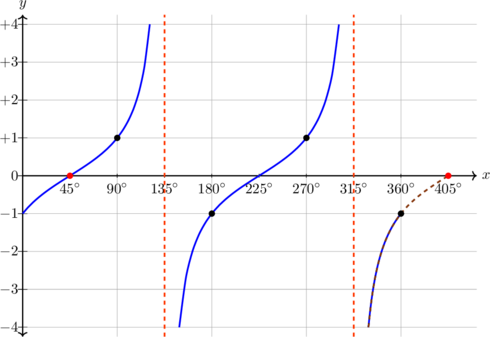
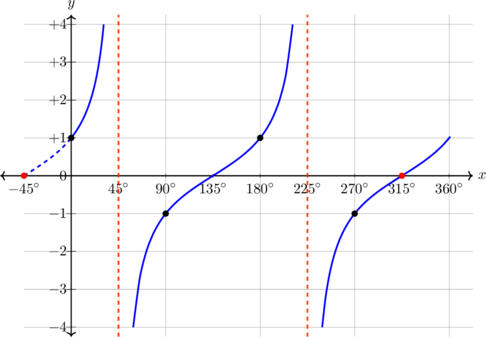
| \(y = \tan (x - 45), \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kanan
Periode = \(180^\text{o}\) Pada x = 90º, y = 1 |
| \(y = \tan (x + 45), \quad 0^\text{o} \leq x \leq 360^\text{o}\)
|
Kurva bergeser 45º ke kiri
Periode = \(180^\text{o}\) Pada x = 0º, y = 1 |
B. PERSAMAAN TRIGONOMETRI
\(\sin x = \sin \alpha\)
Sinus bernilai positif pada kuadran 1 dan 2, maka solusi persamaan terletak pada kuadran 1 dan 2
Solusi 1
\(x = \alpha + k \:.\: 2 \pi\)
Solusi 2
\(x = (\pi - \alpha) + k \:.\: 2 \pi\)
\(\cos x = \cos \alpha \)
Cosinus bernilai positif pada kuadran 1 dan 4, maka solusi persamaan pada kuadran 1 dan 4
Solusi 1
\(x = \alpha + k \:.\: 2 \pi\)
Solusi 2
\(x = - \alpha + k \:.\: 2 \pi\)
\(\tan x = \tan \alpha\)
Tangen bernilai positif pada kuadran 1 dan 3, maka solusi persamaan pada kuadran 1 dan 3, namun dapat disederhanakan menjadi kuadran 1 saja karena bentuk yang berulang
\(\tan x = \tan \alpha\)
\(x = \alpha + k \:.\: \pi\)
k adalah konstanta ..., −3, −2, −1, 0, 1, 2, 3, ...
C. PERTIDAKSAMAAN TRIGONOMETRI
Bentuk pertidaksamaan trigonometri diselesaikan sama seperti persamaan trigonometri untuk menentukan pembuat nol fungsi. Kemudian dilakukan uji titik untuk menentukan tanda positif atau negatif (lihat Latihan Soal).