A. PERSAMAAN GELOMBANG
1. Jenis Gelombang
Berdasarkan mediumnya, gelombang dibedakan atas:
1. Gelombang mekanik
Membutuhkan medium untuk merambat
Contoh: gelombang bunyi, gelombang tali, dll
2. Gelombang elektromagnetik
Tidak membutuhkan medium untuk merambat
Contoh: gelombang cahaya, gelombang radio, dll
Berdasarkan arah getarannya, gelombang dibedakan atas:
1. Gelombang Transversal
Arah getaran tegak lurus dengan arah rambatan
Contoh: gelombang tali, gelombang laut, gelombang elektromagnetik, dll
2. Gelombang Longitudinal
Arah getaran searah dengan arah rambatan
Contoh: gelombang pada pegas, gelombang bunyi, dll
2. Panjang gelombang
Panjang gelombang adalah jarak mendatar antara satu bukit dan satu lembah atau jarak mendatar antara dua puncak gelombang yang berdekatan.
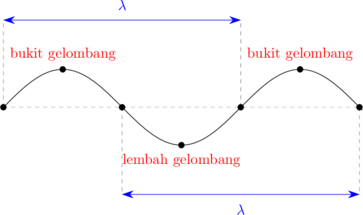
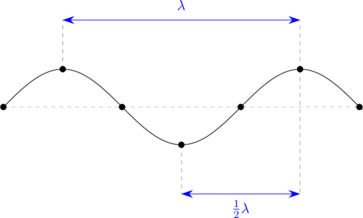
3. Frekuensi dan Periode
Frekuensi adalah banyaknya gelombang dalam satu detik.
Periode adalah waktu yang dibutuhkan untuk satu panjang gelombang.
\(f = \dfrac 1T\) dan \(T = \dfrac 1f\)
4. Cepat Rambat Gelombang
Gelombang adalah rambatan/perjalanan energi. Rambatan energi memiliki kecepatan yang disebut cepat rambat gelombang \(v\).
\(v = \lambda \:.\: f\)
5. Persamaan Gelombang
Persamaan gelombang tanpa fase awal
\(y = A \sin (\omega t - kx)\)
Persamaan gelombang dengan fase awal
\(y = A \sin (\omega t - kx + \theta_{\text{o}})\)
\(y\) = simpangan getar
\(x\) = jarak dari sumber getar
\(A\) = amplitudo
\(t\) = waktu getar
\(\omega\) = kelajuan angular = \(2 \: \pi \:.\: f = \dfrac{2\pi}{T}\)
\(k\) = bilangan gelombang = \(\dfrac{2\pi}{\lambda}\)
\(\theta_{\text{o}}\) = sudut fase awal
6. Kecepatan Dan Percepatan Getaran
Kecepatan Getaran
Kecepatan getaran suatu titik adalah turunan pertama dari persamaan simpangan.
\(v_y = \dfrac{dy}{dt} \)
\(v_y = \omega \:.\: A \:.\: \cos (\omega t - kx) \)
\(v_y = \omega \:.\: \sqrt{A^2 - y^2}\)
Percepatan Getaran
Percepatan getaran suatu titik adalah turunan kedua dari persamaan simpangan.
\(a = \dfrac{d^2y}{dt^2} = \dfrac{dv}{dt} \)
\(a = - \omega^2 \:.\: A \:.\: \sin (\omega t - kx) \)
\(a = - \omega^2 \:.\: y \)
B. FASE DAN SUDUT FASE
Pada suatu persamaan gelombang, \(y = A \sin (\omega t - kx)\)
\(\omega t - kx\) disebut sudut fase \((\theta)\).
\(\bbox[5px, border: 2px solid red] {\theta = \omega t - kx}\)
\begin{equation*} \begin{split} & \theta = \omega t - kx \\\\ & \theta = 2 \pi \:.\: f \:.\: t - \frac {2\pi}{\lambda} \:.\: x) \\\\ & \theta = 2 \pi \left(\frac tT - \frac {x}{\lambda} \right) \end{split} \end{equation*}
\(\dfrac tT - \dfrac {x}{\lambda}\) disebut fase gelombang.
\(\bbox[5px, border: 2px solid red] {\varphi = \dfrac tT - \dfrac {x}{\lambda}}\)
Beda Fase Dua Titik Berbeda Pada Waktu Yang sama
\begin{equation*} \begin{split} \Delta \varphi & = \varphi_2 - \varphi_1 \\\\ \Delta \varphi & = \left(\frac{t}{T} - \frac{x_2}{\lambda}\right) - \left(\frac{t}{T} - \frac{x_1}{\lambda}\right) \\\\ \Delta \varphi & = \cancel {\frac{t}{T}} - \frac{x_2}{\lambda} - \cancel {\frac{t}{T}} + \frac{x_1}{\lambda} \\\\ \Delta \varphi & = \frac{x_1 - x_2}{\lambda} \end{split} \end{equation*}
\(\bbox[5px, border: 2px solid red] {\Delta \varphi = \dfrac{\Delta x}{\lambda}}\)
Beda Fase Suatu Titik Pada Waktu Yang Berbeda
\begin{equation*} \begin{split} \Delta \varphi & = \varphi_2 - \varphi_1 \\\\ \Delta \varphi & = \left(\frac{t_2}{T} - \frac{x}{\lambda}\right) - \left(\frac{t_1}{T} - \frac{x}{\lambda}\right) \\\\ \Delta \varphi & = \frac{t_2}{T} - \cancel {\frac{x}{\lambda}} - \frac{t_1}{T} + \cancel {\frac{x}{\lambda}} \\\\ \Delta \varphi & = \frac{t_2 - t_1}{T} \end{split} \end{equation*}
\(\bbox[5px, border: 2px solid red] {\Delta \varphi = \dfrac{\Delta t}{T}}\)
C. GELOMBANG STATIONER
Gelombang Stationer Ujung Tetap
Persamaan gelombang:
\(y = 2A \sin kx \cos \omega t \)
Amplitudo Gelombang Stationer
\(A_s = 2A \sin kx\)
Letak simpul dari ujung tetap:
\(x = (n - 1) \:.\: \dfrac{\lambda}{2}\)
Letak perut dari ujung tetap:
\(x = \left(n - \dfrac{1}{2}\right) \:.\: \dfrac{\lambda}{2}\)
Jarak antara simpul dan perut yang berdekatan
\(\dfrac {\lambda}{4}\)
Gelombang Stationer Ujung Bebas
Persamaan gelombang:
\(y = 2A \cos kx \sin \omega t\)
Amplitudo Gelombang Stationer
\(A_s = 2A \cos kx\)
Letak simpul dari ujung bebas:
\(x = \left(n - \dfrac{1}{2}\right) \:.\: \dfrac{\lambda}{2}\)
Letak perut dari ujung bebas:
\(x = (n - 1) \:.\: \dfrac{\lambda}{2}\)
Jarak antara simpul dan perut yang berdekatan
\(\dfrac {\lambda}{4}\)