A. GERAK LURUS BERATURAN
1. Jarak dan Perpindahan
Jarak adalah panjang lintasan yang ditempuh.
\(\bbox[10px, border: 2px solid red]{\text{Kelajuan rata-rata} = \dfrac{\text{jarak}}{\text{waktu}}}\)
Perpindahan adalah perubahan posisi tanpa memperhatikan lintasannya.
\(\bbox[10px, border: 2px solid red]{\text{Kecepatan rata-rata} = \dfrac{\text{perpindahan}}{\text{waktu}}}\)
Contoh
Seseorang berjalan dari A menuju D melalui B dan C seperti ditunjukkan pada gambar di bawah ini,

Jarak yang ditempuh orang tersebut adalah \(5 + 10 + 5 = 20 \text{ m}\)
Perpindahan orang adalah \(10 \text{ m}\)
\(\text{Kelajuan rata-rata} = \dfrac{\text{jarak}}{\text{waktu}} = \dfrac{20}{10} = \bbox[5px, border: 2px solid magenta] {2 \text{ m/s}}\)
\(\text{Kecepatan rata-rata} = \dfrac{\text{perpindahan}}{\text{waktu}} = \dfrac{10}{10} = \bbox[5px, border: 2px solid magenta] {1 \text{ m/s}}\)
2. Gerak Lurus Beraturan
Ciri-ciri gerak lurus beraturan
- besar dan arah kecepatan tetap
- percepatan \(a = 0\)
Persamaan
\(\bbox[10px, border: 2px solid red]{s = v \:.\: t}\)
- \(s\) = jarak (m)
- \(v\) = kecepatan (m/s)
- \(t\) = waktu (s)
Grafik
s vs t
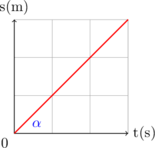
\(v = \tan \alpha\)
v vs t
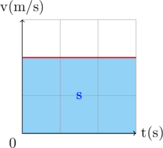
\(s\) = luas di bawah grafik
B. GERAK LURUS BERUBAH BERATURAN
Ciri-ciri Gerak Lurus Berubah Beraturan
- besar kecepatan berubah secara linear
- nilai percepatan ≠ 0 dan bisa bernilai positif atau negatif
Persamaan
- \(s\) = posisi benda (m)
- \(v_{\text{o}}\) = kecepatan mula-mula (m/s)
- \(v_{\text{t}}\) = kecepatan akhir (m/s)
- \(a\) = percepatan (m/s2)
- Dipercepat \(a = (+)\)
- Diperlambat \(a= (-)\)
- \(t\) = waktu (s)
Grafik
s vs t
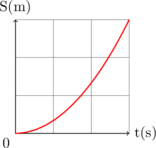
v vs t
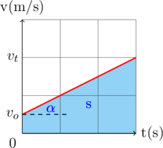
\(s\) = luas di bawah grafik
\(a = \tan \alpha\)
a vs t
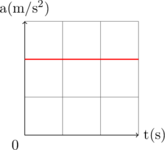
C. GERAK VERTIKAL
Gerak vertikal merupakan gerak lurus beraturan dengan percepatan tetap, yaitu percepatan gravitasi. Karena arah percepatan gravitasi selalu ke arah bawah (ke arah bumi), maka percepatan bernilai minus (\(a = -g\)).
Persamaan

- \(h_o\) = posisi mula-mula (m)
- \(h\) = posisi akhir (m)
- \(v_o\) = kecepatan awal (m/s)
- \(v_t\) = kecepatan akhir (m/s)
- \(g\) = percepatan (m/s2)
- \(t\) = waktu (s)
Grafik
Sebuah benda dilempar vertikal ke atas dari atas tanah dan kemudian jatuh kembali ke tanah, akan memiliki grafik v vs t sebagai berikut:
Kecepatan vs waktu
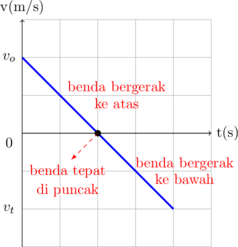
Kecepatan merupakan besaran vektor, sehingga saat benda bergerak ke atas memiliki nilai v (+) dan saat benda bergerak ke bawah memiliki nilai v (−)
Kelajuan vs waktu
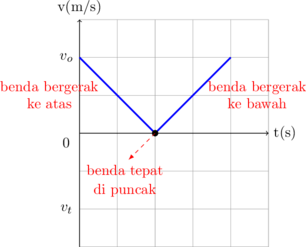
Kelajuan merupakan besaran skalar, sehingga saat benda bergerak ke atas atau ke bawah memiliki nilai v (+)
Gerak Jatuh Bebas
Gerak jatuh bebas merupakan gerak benda yang dijatuhkan dari ketinggian tertentu tanpa kecepatan awal \(\bbox[10px, border: 2px solid red]{(v_o = 0)}\)
