A. TURUNAN TRIGONOMETRI
| \(f(t)\) | \(f'(t)\) |
|---|---|
| \(\sin t\) | \(\cos t\) |
| \(\cos t\) | \(- \sin t\) |
Tentukan turunan pertama dari \(y = \sin \: (2t + 5)\)
\begin{equation*} \begin{split} & y = \sin \: ({\color {red} 2t + 5}) \\\\ & {\color {blue} \text{turunan dari } \sin \: (2t + 5) \text{ adalah } \cos \: (2t + 5)} \\\\ & {\color {blue} \text{turunan dari } 2t + 5 \text{ adalah } 2} \\\\ & \bbox[5px, border: 2px solid magenta] {\frac {dy}{dt} = y' = 2 \:.\: \cos \: (2t + 5)} \end{split} \end{equation*}
B. PERSAMAAN GETARAN
| Besaran | Persamaan | Max | Max |
|---|---|---|---|
| Simpangan | \(y = A \sin (\omega t + \theta)\) | Benda berada di titik terjauh
\(y_{\text{max}} = A\) |
Benda berada di titik seimbang
\(y_{\text{min}} = 0\) |
| Kecepatan (1) | \(v = \dfrac {dy}{dy}\)
\(v = \omega A \cos (\omega t + \theta)\) |
Benda berada di titik seimbang
\(v_{\text{max}} = \omega A\) |
Benda berada di titik terjauh
\(v_{\text{min}} = 0\) |
| Kecepatan (2) | \(v = \omega \sqrt{A^2 - y^2}\) | ||
| Percepatan | \(a = \dfrac {dv}{dt}\)
\(a = - \omega^2 A \sin (\omega t + \theta)\) \(a = - \omega^2 y\) |
Benda berada di titik terjauh
\(a_{\text{max}} = \omega^2 A\) |
Benda berada di titik seimbang
\(a_{\text{min}} = 0\) |
| Energi Potensial | \(E_p = \dfrac 12 ky^2\) | Benda berada di titik terjauh
\(E_{\text{p max}} = \dfrac 12 kA^2\) |
Benda berada di titik seimbang
\(E_{\text{p min}} = 0\) |
| Energi Kinetik | \(E_k = \dfrac 12 mv^2\) | Benda berada di titik seimbang
\(E_{\text{k max}} = \dfrac 12 kA^2\) |
Benda berada di titik terjauh
\(E_{\text{k min}} = 0\) |
| Energi Mekanik | \(E_M = E_p + E_k\)
Besar energi mekanik selalu tetap. Pada saat energi potensial mencapai maksimum, energi kinetiknya sama dengan nol. Pada saat energi kinetik mencapai maksimum, energi potensialnya sama dengan nol. Maka dapat disimpulkan \(E_M = E_{\text{p max}} = E_{\text{k max}}\) |
||
Keterangan
\(y\) = simpangan (jarak partikel dari titik seimbangnya) ... m atau cm
\(A\) = amplitudo (simpangan terjauh/simpangan maksimum) ... m atau cm
\(\omega\) = kecepatan sudut/frekuensi sudut ... rad/s
\(ω = 2 \pi \: f = \dfrac{2 \pi}{T}\) ... rad/s
\(f\) = frekuensi = banyaknya getaran setiap detik ... Hz
\(T\) = periode = waktu yang dibutuhkan untuk 1 getaran ... detik
\(t\) = waktu sumber getar
\(\theta_o\) = sudut fase mula-mula
C. GAYA PEMULIH
Gaya pemulih adalah gaya yang mondorong/menarik partikel agar kembali ke titik seimbang. Oleh karena itu, arah gaya pemulih selalu menuju titik seimbang. Besar gaya pemulih:
\(F = m \:.\:a\)
\(F = m \:.\: -\omega^2 \:.\: y\)
\(F = -m \:.\: \omega^2 \:.\: y\)
Tanda (−) menunjukkan arah gaya pemulih berlawanan dengan arah getaran.
Gaya Pemulih Pada Bandul
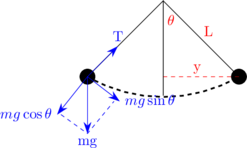
Gaya pemulih pada bandul = \(F = -m \:.\: g \:.\: \sin \theta\)
Arah gaya pemulih selalu menuju titik seimbang.
\begin{equation*} \begin{split} & F = m \:.\: a \\\\ & -\cancel{m} \:.\: g \:.\: \sin \theta = \cancel{m} \:.\: -\omega^2 \:.\: y\\\\ & g \:.\: \frac{\cancel{y}}{L} = \omega^2 \:.\: \cancel{y}\\\\ & \frac{g}{L} = \omega^2\\\\ & \omega = \sqrt{\frac{g}{L}}\\\\ & 2 \pi \:.\: f = \sqrt{\frac{g}{L}}\\\\ & f = \frac{1}{2\pi}\sqrt{\frac{g}{L}}\\\\ & \bbox[10px, border: 2px solid red]{T =2\pi\sqrt{\frac{L}{g}}} \end{split} \end{equation*}
Gaya Pemulih Pada Pegas

Gaya pemulih pada pegas = \(F = -k \:.\: y\)
Arah gaya pemulih selalu menuju titik seimbang.
\begin{equation*} \begin{split} & F = m \:.\: a \\\\ & -k \:.\: y = m \:.\: -\omega^2 \: y\\\\ & k = m \:.\: \omega^2 \\\\ & \omega^2 = \frac{k}{m}\\\\ & \omega = \sqrt{\frac{k}{m}}\\\\ & 2 \pi \: f = \sqrt{\frac{k}{m}}\\\\ & f = \frac{1}{2\pi}\sqrt{\frac{k}{m}}\\\\ & \bbox[10px, border: 2px solid red]{T =2\pi\sqrt{\frac{m}{k}}} \end{split} \end{equation*}
