A. GAYA GRAVITASI
Dua buah benda akan saling tarik menarik dengan gaya yang besarnya berbanding lurus dengan massa kedua benda
dan berbanding terbalik dengan kuadrat jarak kedua benda

\(\bbox[5px, border: 2px solid red]{F = G \: \dfrac {m_A \:.\: m_B}{r^2}}\)
\(F_{AB}\) dan \(F_{BA}\) sama besar namun berlawanan arah
B. MEDAN GRAVITASI
Medan gravitasi adalah pengaruh gravitasi yang ditimbulkan oleh suatu benda di sekeliling benda tersebut.
Kuat medan gravitasi (E) adalah besarnya pengaruh gravitasi oleh benda bermassa M, pada suatu titik yang berjarak r dari benda tersebut.
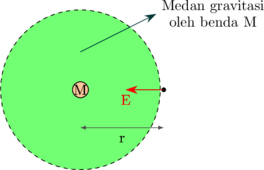
\(\bbox[5px, border: 2px solid red]{E = G \: \dfrac {M}{r^2}}\)
Arah kuat medan gravitasi dari titik menuju ke benda
Kuat medan gravitasi (E) sering juga disebut sebagai percepatan gravitasi (g).
Satuan untuk kuat medan gravitasi adalah N/kg atau m/s².
C. ENERGI POTENSIAL GRAVITASI
1. Energi Potensial Gravitasi
Energi potensial gravitasi adalah energi yang timbul di antara dua benda akibat gaya tarik gravitasi satu sama lain.
\(U = - \dfrac {M \:.\: m}{r}\)
Nilai energi potensial gravitasi \(U \leq 0\)
Penjelasan mengenai tanda (−) pada energi potensial gravitasi
Bentuk lain dari energi potensial gravitasi adalah \(EP = mgh\), dan rumus tersebut memiliki tanda (+). Rumus \(EP = mgh\) menggunakan kerangka acuan permukaan bumi.
Energi potensial gravitasi dengan rumus \(U = - \dfrac {M \:.\: m}{r}\) digunakan untuk jarak yang sangat besar (alam semesta) dan menggunakan kerangka acuan tak berhingga.
Kedua rumus \(EP = mgh\) dan \(U = - \dfrac {M \:.\: m}{r}\) memiliki arti yang sama.

B. Escape Velocity
Escape velocity adalah kecepatan minimum yang dibutuhkan untuk dapat lepas dari gravitasi bumi.
Misalkan sebuah roket yang akan diluncurkan dari permukaan bumi ke luar angkasa. Dibutuhkan usaha luar dari roket untuk membebaskan roket dari gravitasi bumi.
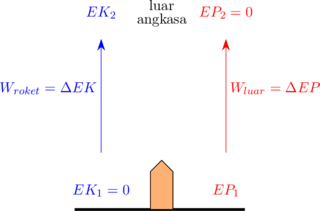
\begin{equation*} \begin{split} & W_{\text{roket}} = W_{\text{luar}} \\\\ & \Delta EK = \Delta EP \\\\ & EK_2 - EK_1 = EP_2 - EP_1 \\\\ & EK_2 - 0 = 0 - EP_1 \\\\ & EK_2 = - EP_1 \\\\ & \frac 12 \:.\: \cancel {m} \:.\: v^2 = G \: \frac {M \:.\: \cancel {m}}{R} \quad \dotso \text{ m = massa roket}\\\\ & \bbox[5px, border: 2px solid red]{v = \sqrt{\frac {2GM}{R}} \quad \dotso \text{ M = massa bumi}} \end{split} \end{equation*}
D. HUKUM KEPPLER
Hukum Keppler 1
Orbit planet yang mengelilingi matahari berbentuk elips dimana matahari berada pada salah satu fokus elips
Hukum Keppler 2
Radius planet mengelilingi matahari membentuk luas yang sama besar pada interval waktu yang sama
Hukum Keppler 3
Perbandingan kuadrat dari periode dua planet sama besar dengan perbandingan pangkat tiga dari radius lintasan kedua planet tersebut
\(\left(\dfrac {T_A}{T_B}\right)^2 = \left(\dfrac {R_A}{R_B}\right)^3\)
Orbit Satelit
Gaya gravitasi antara planet dan satelit menyebabkan satelit dapat mengitari planet. Gaya gravitasi tersebut merupakan gaya sentripetal yang bekerja pada benda yang bergerak melingkar beraturan.
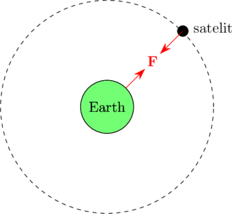
Kecepatan orbit satelit
\begin{equation*} \begin{split} & F_{\text{sentripetal}} = F_{\text{gravitasi}} \\\\ & m_{\text{satelit}} \: \frac{v^2}{R} = G \:.\: \frac{M_{\text{bumi}} \:.\: m_{\text{satelit}}}{R^2} \\\\ & \cancel {m_{\text{satelit}}} \: \frac{v^2}{R} = G \:.\: \frac{M_{\text{bumi}} \:.\: \cancel {m_{\text{satelit}}}}{R^2} \\\\ & \frac{v^2}{R} = G \:.\: \frac{M_{\text{bumi}}}{R^2} \\\\ & v^2 = G \:.\: \frac{M_{\text{bumi}}}{R} \\\\ & \bbox[5px, border: 2px solid red]{v = \sqrt{G \:.\: \frac{M_{\text{bumi}}}{R}}} \end{split} \end{equation*}
Periode satelit
\begin{equation*} \begin{split} & F_{\text{sentripetal}} = F_{\text{gravitasi}} \\\\ & \cancel {m_{\text{satelit}}} \:.\: \omega^2 \:.\: R = G \:.\: \frac{M_{\text{bumi}} \:.\: \cancel {m_{\text{satelit}}}}{R^2} \\\\ & \omega^2 \:.\: R = G \:.\: \frac{M_{\text{bumi}}}{R^2} \\\\ & \omega^2 = G \:.\: \frac{M_{\text{bumi}}}{R^3} \\\\ & \omega = \sqrt{G \:.\: \frac{M_{\text{bumi}}}{R^3}} \\ & \frac{2 \pi}{T} = \sqrt{G \:.\: \frac{M_{\text{bumi}}}{R^3}} \\\\ & \frac{T}{2 \pi} = \sqrt{\frac{R^3}{GM_{\text{bumi}}}} \\\\ & \bbox[5px, border: 2px solid red]{T = 2 \pi \:.\: \sqrt{\frac{R^3}{GM_{\text{bumi}}}}} \end{split} \end{equation*}
Perbandingan periode 2 satelit
\begin{equation*} \begin{split} & T = 2 \pi \sqrt{\frac{R^3}{GM}} \\\\ & T^2 = 4 \pi^2 \:.\: \frac{R^3}{GM} \\\\ & \frac{(T_A)^2}{(T_B)^2} = \frac{ \cancel {4 \pi^2} \cdot \dfrac{(R_A)^3}{\cancel{GM}}}{ \cancel {4 \pi^2} \:.\: \dfrac{(R_B)^3}{\cancel {GM}}} \\\\ & \bbox[5px, border: 2px solid red]{\left(\frac{T_A}{T_B}\right)^2 = \left(\frac{R_A}{R_B}\right)^3} \end{split} \end{equation*}
