A. HUKUM-HUKUM NEWTON
Hukum Newton 1
Jika resultan gaya-gaya yang bekerja pada sebuah benda sama dengan NOL, maka benda akan tetap diam atau bergerak lurus beraturan
\(\sum F = 0\)
Hukum ini sering disebut Hukum Kelembaman, dimana setiap benda cenderung untuk mempertahankan keadaannya semula. Bila suatu benda mula-mula diam, benda tersebut akan cenderung untuk tetap diam. Sebaliknya, bila suatu benda sedang bergerak, maka benda tersebut cenderung untuk tetap bergerak.
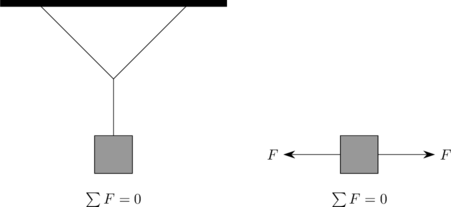
Hukum Newton 2
Gaya yang bekerja pada suatu benda berbanding lurus dengan perubahan momentum per satuan waktu
\(F = \dfrac {\Delta p}{\Delta t}\)
Karena momentum, \(p\) adalah massa dikali kecepatan, maka:
\begin{equation*} \begin{split} & F = \frac {\Delta p}{\Delta t} \\\\ & F = \frac {mv_t - mv_o}{\Delta t} \\\\ & F = \frac {m (v_t - v_o)}{\Delta t} \\\\ & \bbox[10px, border: 2px solid red]{F = m \:.\: a} \end{split} \end{equation*}
Hukum kedua Newton diaplikasikan pada benda-benda yang bergerak lurus berubah beraturan (GLBB). Maka persamaan pada GLBB kadang diperlukan pada beberapa jenis soal tertentu.
\(S = v_o \:.\: t + \frac 12 \:.\: a \:.\: t^2\)
\(v_t = v_o + a \;.\:t\)
\(v_t^2 = v_o^2 + 2 \:.\: a \:.\: s\)
Hukum Newton 3
Jika benda A memberikan gaya FA ke benda B, maka benda B akan memberikan gaya FB yang nilainya sama besar dan arah yang berlawanan ke benda A
\(F_A = - F_B\)
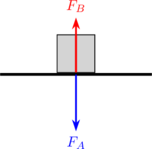
FA adalah gaya yang diberikan kotak pada lantai.
FB adalah gaya yang diberikan lantai pada kotak.
Saat kotak memberi gaya pada lantai (FA), maka lantai akan memberi gaya yang sama besar pada kotak (FB)
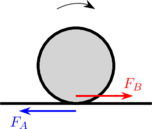
FA adalah gaya yang diberikan roda pada lantai.
FB adalah gaya yang diberikan lantai pada roda.
Saat roda berputar, roda memberikan gaya FA ke lantai, dan lantai memberikan gaya ke FB roda.
Hukum Newton III merupakan pasangan gaya yang bekerja pada dua benda. Dengan kata lain, gaya-gaya yang bekerja pada benda selalu berpasangan.
Hukum Newton III sering disebut sebagai Hukum aksi reaksi, dimana untuk setiap FAksi, akan ada FReaksi yang besarnya sama dan arahnya berlawanan.
B. GAYA NORMAL DAN GAYA GESEKAN
1. Gaya Normal
Gaya normal adalah gaya yang muncul apabila benda bersentuhan dengan permukaan bidang.
Arah gaya normal selalu tegak lurus dengan bidang permukaannya.
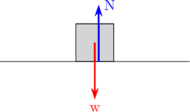
\begin{equation*} \begin{split} &\Sigma F = 0 \\\\ & N - w = 0 \\\\ & N = w \end{split} \end{equation*}
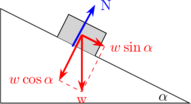
\begin{equation*} \begin{split} & \Sigma F_y = 0 \\\\ & N - w \cos \alpha = 0 \\\\ & N = w \cos \alpha \end{split} \end{equation*}
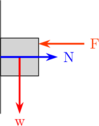
\begin{equation*} \begin{split} & \Sigma F_x = 0 \\\\ & N - F = 0 \\\\ & N = F \end{split} \end{equation*}
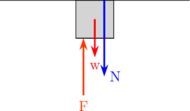
\begin{equation*} \begin{split} & \Sigma F_y = 0 \\\\ & F - w - N = 0 \\\\ & N = F - w \end{split} \end{equation*}
2. Gaya Gesekan
Gaya gesekan terjadi pada dua buah bidang yang saling bergesekan. Besarnya gaya gesekan ditentukan oleh koefisien gesekan μ (tingkat kekasaran kedua bidang) dan gaya normal antara kedua bidang tersebut. Umumnya koefisien gesekan dari benda yang sedang diam lebih besar daripada koefisien gesekan dari benda yang sedang bergerak.
Gaya gesekan dapat dibedakan menjadi:
1. Gaya gesekan statis
Gaya gesekan statis muncul pada benda yang sedang diam dan dikenai gaya tertentu.
Besar gaya gesekan statis tergantung dari besar gaya yang bekerja, dengan nilai maksimum sebesar \(\bbox[10px, border: 2px solid red]{f_{s \text{ max}} = \mu_s \:.\: N}\)
2. Gaya gesekan dinamis
Gaya gesekan dinamis muncul pada benda yang sedang bergerak.
Besar gaya gesekan dinamis adalah \(\bbox[10px, border: 2px solid red]{f_k = \mu_k \:.\: N}\)
Arah gaya gesekan selalu berlawanan dengan arah gerak benda (bila benda tersebut sedang bergerak) atau berlawanan dengan arah gaya yang dikenai pada benda tersebut (jika benda sedang diam).
![]()
3. Lift
Saat seseorang berada di dalam lift, orang tersebut memberikan gaya tekan pada lantai lift, dan lantai memberikan gaya reaksi yang berlawanan arah (dinyatakan dalam N).
LIFT DIAM ATAU BERGERAK LURUS BERATURAN
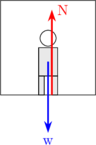
\begin{equation*} \begin{split} \Sigma F & = 0 \\\\ N - w & = 0 \\\\ N & = m \:.\: g \end{split} \end{equation*}
LIFT DIPERCEPAT KE ATAS
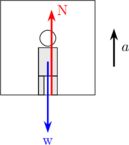
\begin{equation*} \begin{split} \Sigma F & = m \:.\: a \\\\ N - w & = m \:.\: a \\\\ N & = m \:.\: g + m \:.\: a \end{split} \end{equation*}
LIFT DIPERLAMBAT KE ATAS
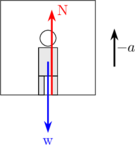
\begin{equation*} \begin{split} \Sigma F & = m \:.\: a \\\\ N - w & = m \:.\: -a \\\\ N & = m \:.\: g - m \:.\: a \end{split} \end{equation*}
LIFT DIPERCEPAT KE BAWAH
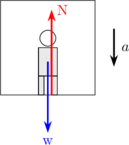
\begin{equation*} \begin{split} \Sigma F & = m \:.\: a \\\\ w - N & = m \:.\: a \\\\ N & = m \:.\: g - m \:.\: a \end{split} \end{equation*}
LIFT DIPERLAMBAT KE BAWAH
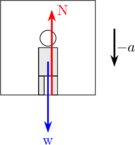
\begin{equation*} \begin{split} \Sigma F & = m \:.\: a \\\\ w - N & = m \:.\: -a \\\\ N & = m \:.\: g + m \:.\: a \end{split} \end{equation*}
4. Dua Benda Bertumpuk
Dua benda bertumpuk
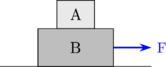
Diagram gaya
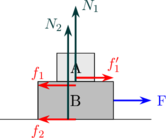
Pada kasus dua benda yang bertumpuk, terjadi gesekan antara permukaan kedua benda yang saling bersentuhan \(f_1\) dan \(f_1'\), dimana \(f_1\) dan\(f_1'\) merupakan gaya aksi-reaksi yang sama besar dan berlawanan arah. Gaya gesekan \(f_1\) dan \(f_2\) bekerja pada benda B dan \(f_1'\) bekerja pada benda A.
Gaya gesekan juga terdapat antara benda B dan lantai \(f_2\).
Tinjau sistem
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & F - f_1 + f_1' - f_2 = (m_A + m_B) \:.\: a \\\\ & F - f_2 = (m_A + m_B) \:.\: a \end{split} \end{equation*}
Tinjau Benda A
\begin{equation*} \begin{split} & \Sigma F = m_A \:.\: a \\\\ & f_1' = m_A \:.\: a \end{split} \end{equation*}
Tinjau Benda B
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & F - f_1 - f_2 = m_B \:.\: a \end{split} \end{equation*}
C. BIDANG MIRING
Diagram gaya bidang miring
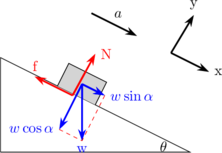
\begin{equation*} \begin{split} & \Sigma F_y = 0 \\\\ & N - w \:.\: \cos \theta = 0 \\\\ & N = w \:.\: \cos \theta \end{split} \end{equation*}
\begin{equation*} \begin{split} & \Sigma F_x = m \:.\: a \\\\ & w \:.\: \sin \theta - f_k = m \:.\: a \\\\ & w \:.\: \sin \theta - \mu_k \:.\: N = m \:.\: a \end{split} \end{equation*}
D. GAYA KONTAK DAN TEGANGAN TALI
1. Gaya Kontak
Pada dua buah benda yang berhimpitan, muncul gaya kontak antara kedua benda, sebagai akibat dari gaya aksi - reaksi.
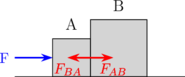
Gaya kontak \(F_{BA}\) (bekerja pada benda A) dan \(F_{AB}\) (bekerja pada benda B) sama besar dan berlawanan arah.
Tinjau sistem
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & F - F_{BA} + F_{AB} = (m_A + m_B) \:.\: a \\\\ & F = (m_A + m_B) \:.\: a \end{split} \end{equation*}
Tinjau Benda A
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & F - F_{BA} = m_A \:.\: a \end{split} \end{equation*}
Tinjau Benda B
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & F_{AB} = m_B \:.\: a \end{split} \end{equation*}
2. TEGANGAN TALI
Dua buah benda dihubungkan dengan tali dan ditarik oleh gaya F seperti gambar di bawah ini:
![]()
Gaya tegangan tali digambarkan sebagai panah yang saling berhadap-hadapan.
Pada benda A, bekerja gaya tegangan tali T ke arah kanan.
Pada benda B, bekerja gaya F ke arah kanan dan gaya tegangan tali T ke arah kiri.
Tegangan tali yang bekerja pada benda A dan benda B sama besar.
Tinjau sistem
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & F - T + T = (m_A + m_B) \:.\: a \\\\ & F = (m_A + m_B) \:.\: a \end{split} \end{equation*}
Tinjau Benda A
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & T = m_A \:.\: a \end{split} \end{equation*}
Tinjau Benda B
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & F - T = m_B \:.\: a \end{split} \end{equation*}
3. Katrol
Pada gambar di bawah ini, dua buah benda dihubungkan dengan tali dan digantungkan pada sebuah katrol permanen. Katrol diasumsikan licin sehingga saat tali bergerak, katrol tidak berotasi.
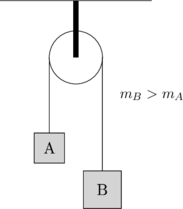
Jika diasumsikan \(m_B > m_A\), maka benda A akan bergerak ke atas dan benda B akan bergerak ke bawah dengan percepatan yang sama besar. Tegangan tali yang terhubung pada kedua benda juga sama besar.
Diagram gaya
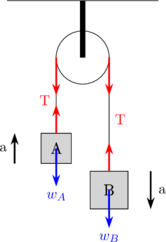
Tinjau sistem
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & w_B - w_A = (m_A + m_B) \:.\: a \end{split} \end{equation*}
Tinjau benda A
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & T - w_A = m_A \:.\: a \end{split} \end{equation*}
Tinjau benda B
\begin{equation*} \begin{split} & \Sigma F = m \:.\: a \\\\ & w_B - T = m_B \:.\: a \end{split} \end{equation*}
E. GAYA SENTRIPETAL
1. Percepatan Sentripetal
Percepatan sentripetal adalah percepatan yang muncul pada benda yang bergerak melingkar dan arahnya menuju pusat lingkaran.
Kecepatan linear tegak lurus dengan radius lingkaran.
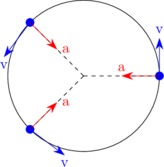
\(\bbox[10px, border: 2px solid red]{a_s = \dfrac {v^2}{R} = \omega^2 \:.\: R}\)
2. Gaya sentripetal
Sama seperti percepatan sentripetal, gaya sentripetal juga bekerja pada benda yang bergerak melingkar dan arahnya menuju pusat lingkaran.
\(F_s = m \:.\: a_s\)
\(\bbox[10px, border: 2px solid red]{F_s = m \:.\: \dfrac {v^2}{R} = m \:.\: \omega^2 \:.\: R}\)
3. Ayunan Konis
Sebuah batu diikat pada ujung tali dan diputar horizontal seperti gambar di bawah ini:

Diagram gaya
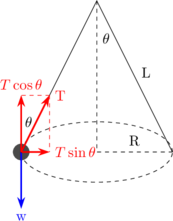
\begin{equation*} \begin{split} \Sigma F_x & = m \:.\: a_s \\\\ T \sin \theta & = m \:.\: \frac {v^2}{R} \quad {\color {red} \dotso \: (1)} \end{split} \end{equation*}
\begin{equation*} \begin{split} \Sigma F_y & = 0 \\\\ T \cos \theta & = m \:.\: g \quad {\color {red} \dotso \: (2)} \end{split} \end{equation*}
Eliminasi persamaan (1) dan (2)
\begin{equation*} \begin{split} \frac {\cancel{T} \sin \theta}{\cancel{T} \cos \theta} & = \frac {m \:.\: \dfrac {v^2}{R}}{m \:.\: g } \\\\ \tan \theta & = \frac {\dfrac {v^2}{R}}{g} \\\\ \tan \theta & = \frac {v^2}{g R} \\\\ v^2 & = gR \tan \theta \\\\ v & = \sqrt{gR \tan \theta} \end{split} \end{equation*}
\begin{equation*} \begin{split} \sin \theta & = \frac {R}{L} \\\\ R & = L \sin \theta \end{split} \end{equation*}
4. Tikungan jalan dengan kemiringan θ
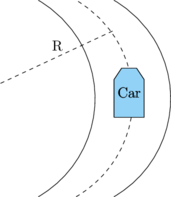
Diagram gaya
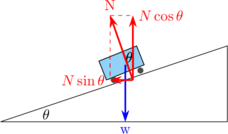
\begin{equation*} \begin{split} & \Sigma F_x = m \:.\: a_s \\\\ & N \sin \theta = m \:.\: \frac {v^2}{R} \quad {\color {red} \dotso \: (1)} \end{split} \end{equation*}
\begin{equation*} \begin{split} & \Sigma F_y = 0 \\\\ & N \cos \theta = m \:.\: g \quad {\color {red} \dotso \: (2)} \end{split} \end{equation*}
Eliminasi persamaan (1) dan (2)
\begin{equation*} \begin{split} & \frac {\cancel{N} \sin \theta}{\cancel{N} \cos \theta} = \frac {\cancel{m} \:.\: \dfrac {v^2}{R}}{\cancel{m} \:.\: g } \\\\ & \tan \theta = \frac {\dfrac {v^2}{R}}{g} \\\\ & \tan \theta = \frac {v^2}{g \:.\: R} \\\\ & v^2 = g \:.\: R \:.\: \tan \theta \\\\ & v = \sqrt{g \:.\: R \:.\: \tan \theta} \end{split} \end{equation*}
5. Tikungan jalan dengan koefisien gesekan μ

Diagram gaya
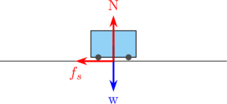
\begin{equation*} \begin{split} & \Sigma F_x = m \:.\: a_s \\\\ & f_s = m \:.\: a_s \\\\ & \mu_s \:.\: N = m \:.\: \frac {v^2}{R} \quad {\color {red} \dotso \: (1)} \end{split} \end{equation*}
\begin{equation*} \begin{split} & \Sigma F_y = 0 \\\\ & N = m \:.\: g \quad {\color {red} \dotso \: (2)} \end{split} \end{equation*}
Eliminasi persamaan (1) dan (2)
\begin{equation*} \begin{split} & \frac {\mu_s \:.\: \cancel{N}}{\cancel{N}} = \frac {\cancel{m} \:.\: \dfrac {v^2}{R}}{\cancel{m} \:.\: g } \\\\ & \mu_s = \frac {\dfrac {v^2}{R}}{g} \\\\ & \mu_s = \frac {v^2}{g \:.\: R} \\\\ & v^2 = g \:.\: R \:.\: \mu_s \\\\ & v = \sqrt{g \:.\: R \:.\: \mu_s} \end{split} \end{equation*}
