A. IMPULS DAN MOMENTUM
1. Impuls
\(\bbox[10px, border: 2px solid red]{I = F \:.\: \Delta t}\)
I = impuls ... Ns
F = gaya ... N
Δt = selang waktu ... s
2. Momentum
\(\bbox[10px, border: 2px solid red]{p = m \:.\: v}\)
p = momentum ... kg m/s
m = massa ... kg
v = kecepatan ... m/s
3. Impuls dan Perubahan Momentum
\begin{equation*} \begin{split} & I = \Delta p \\\\ & I = p_2 - p_1 \\\\ & I = mv_2 - mv_1 \\\\ & \bbox[10px, border: 2px solid red]{I = m(v_2 - v_1)} \end{split} \end{equation*}
4. Grafik F vs Δt
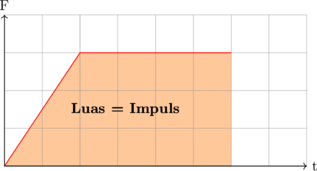
Luas di bawah grafik adalah besar impuls yang dihasilkan
B. HUKUM KEKEKALAN MOMENTUM
Pada interaksi dua buah benda A dan B, total momentum sebelum interaksi sama dengan total momentum sesudah interaksi.
\(\bbox[10px, border: 2px solid red]{p_A + p_B = p_A' + p_B'}\)
Bila lintasan benda berada dalam satu garis lurus, hukum kekekalan momentum dapat dituliskan sebagai berikut:
\(m_A \:.\: v_A + m_B \:.\: v_B = m_A \:.\: v_A' + m_B \:.\: v_B' \)
C. KOEFISIEN RESTITUSI
1. Tumbukan dua benda
Pada tumbukan antara dua benda, dikenal istilah koefisien restitusi (e), yaitu:
\(\bbox[10px, border: 2px solid red]{e = \dfrac {v_B' - v_A'}{v_A - v_B}}\)
Nilai koefisien restitusi \(0 \leq e \leq 1\) yang besarnya tergantung dari jenis tumbukan.
2. Pantulan bola
Sebuah benda jatuh bebas dari ketinggian \(h_o\), menumbuk lantai dan memantul kembali pada ketinggian \(h_1\), maka:
\(\bbox[10px, border: 2px solid red]{e = \sqrt{\dfrac {h_1}{h_o}} = \sqrt{\dfrac {h_2}{h_1}} = \dotso}\)
e = koefisien restitusi
Tinggi pantulan ke n
\(h_n = e^{2n} \:.\: h_o\)
