Terdapat 4 jenis irisan kerucut:
1. Parabola (e = 1)
2. Lingkaran (e = 1)
3. Elips (e < 1)
4. Hiperbola (e > 1)
Parabola dan lingkaran dibahas pada bab terpisah. Pada bab ini, khusus untuk membahas elips dan hiperbola.
A. ELIPS
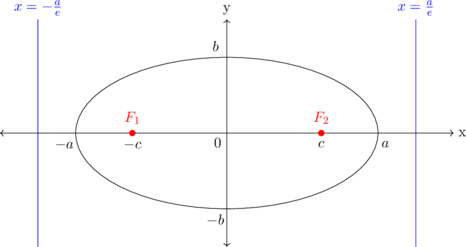
SUMBU MAYOR PADA ARAH X
| Pusat (0,0) | Pusat (h,k) | |
|---|---|---|
|
|
\(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\), dimana \(a > b\)
Pusat: \((0,0)\) Vertices: \((\pm a,0), (0, \pm b)\) Fokus: \((\pm c,0)\) Direktriks: \(x = \pm \dfrac ae\) \(e = \dfrac ca\) \(c^2 = a^2 - b^2\)
|
\(\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1\), dimana \(a > b\)
Pusat: \((h,k)\) Vertices: \((h \pm a,k), (h, k \pm b)\) Fokus: \((h \pm c,k)\) Direktriks: \(x = h \pm \dfrac ae\) \(e = \dfrac ca\) \(c^2 = a^2 - b^2\)
|
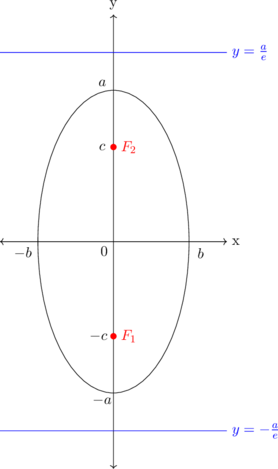
SUMBU MAYOR PADA ARAH Y
| Pusat (0,0) | Pusat (h,k) | |
|---|---|---|
|
|
\(\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1\), dimana \(a > b\)
Pusat: \((0,0)\) Vertices: \((0,\pm a), (\pm b,0)\) Fokus: \((0, \pm c)\) Direktriks: \(y = \pm \dfrac ae\) \(e = \dfrac ca\) \(c^2 = a^2 - b^2\)
|
\(\dfrac{(x-h)^2}{b^2} + \dfrac{(y-k)^2}{a^2} = 1\), dimana \(a > b\)
Pusat: \((h,k)\) Vertices: \((h,k \pm a), (h \pm b,k)\) Fokus: \((h,k \pm c)\) Direktriks: \(y = k \pm \dfrac ae\) \(e = \dfrac ca\) \(c^2 = a^2 - b^2\)
|
B. HIPERBOLA
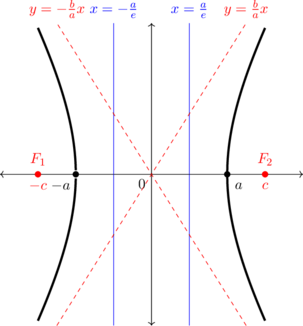
SUMBU MAYOR PADA ARAH X
| Pusat (0,0) | Pusat (h,k) | |
|---|---|---|
|
|
\(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\)
Pusat: \((0,0)\) Vertices: \((\pm a,0)\) Fokus: \((\pm c,0)\) Direktriks: \(x = \pm \dfrac ae\) Asimtot: \(y = \pm \dfrac ba x\) \(e = \dfrac ca\) \(c^2 = a^2 + b^2\)
|
\(\dfrac{(x-h)^2}{a^2} - \dfrac{(y-k)^2}{b^2} = 1\)
Pusat: \((h,k)\) Vertices: \((h \pm a,k)\) Fokus: \((h \pm c,k)\) Direktriks: \(x = h \pm \dfrac ae\) Asimtot: \(y - k = \pm \dfrac ba (x - h)\) \(e = \dfrac ca\) \(c^2 = a^2 + b^2\)
|
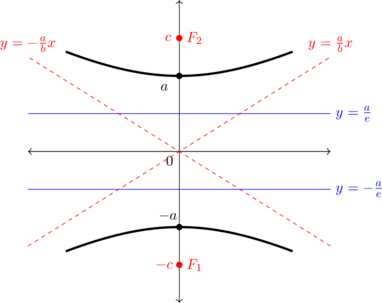
SUMBU MAYOR PADA ARAH Y
| Pusat (0,0) | Pusat (h,k) | |
|---|---|---|
|
|
\(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\)
Pusat: \((0,0)\) Vertices: \((0,\pm a)\) Fokus: \((0,\pm c) \) Direktriks: \(y = \pm \dfrac ae\) Asimtot: \(y = \pm \dfrac ab x\) \(c^2 = a^2 - b^2\) \(e = \dfrac ca\) |
\(\dfrac{(y-k)^2}{a^2} - \dfrac{(x-h)^2}{b^2} = 1\)
Pusat: \((h,k)\) Vertices: \((h,k \pm a)\) Fokus: \((h,k \pm c) \) Direktriks: \(y = k \pm \dfrac ae\) Asimtot: \(y - k = \pm \dfrac ab (x - h)\) \(c^2 = a^2 - b^2\) \(e = \dfrac ca\) |
A. Elips B. Hiperbola C. Persiapan Ulangan Kembali ke Modul SMA