A. SIFAT-SIFAT LIMIT
\(\displaystyle \lim_{x \rightarrow a} f(x)= k\)
Saat nilai x mendekati a, maka nilai f(x) mendekati k
Perhatikan grafik di bawah ini:
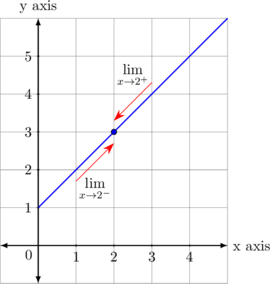
Saat nilai x mendekati 2 dari arah kiri, nilai y mendekati 3
\(\displaystyle \lim_{x \rightarrow 2^{-}} f(x)= 3\)
Saat nilai x mendekati 2 dari arah kanan, nilai y mendekati 3
\(\displaystyle \lim_{x \rightarrow 2^{+}} f(x)= 3\)
Karena \(\displaystyle \lim_{x \rightarrow 2^{-}} f(x) = \displaystyle \lim_{x \rightarrow 2^{+}} f(x)\), maka dapat ditulis sebagai:
\(\displaystyle \lim_{x \rightarrow 2} f(x) = 3\)
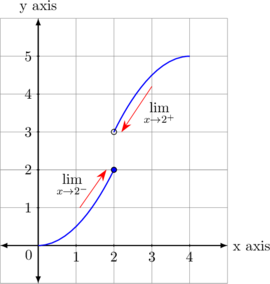
Saat nilai x mendekati 2 dari arah kiri, nilai y mendekati 2
\(\displaystyle \lim_{x \rightarrow 2^{-}} f(x)= 2\)
Saat nilai x mendekati 2 dari arah kanan, nilai y mendekati 3
\(\displaystyle \lim_{x \rightarrow 2^{+}} f(x)= 3\)
Karena \(\displaystyle \lim_{x \rightarrow 2^{-}} f(x) \neq \displaystyle \lim_{x \rightarrow 2^{+}} f(x)\), maka:
\(\displaystyle \lim_{x \rightarrow 2} f(x) = \text{tidak ada} \)
Contoh 01
Diketahui \(f(x) = \dfrac {x - 5}{x + 1}\)
Tentukan:
(A) \(\displaystyle \lim_{x \rightarrow 5^-} f(x) \)
(B) \(\displaystyle \lim_{x \rightarrow 5^+} f(x) \)
(C) \(\displaystyle \lim_{x \rightarrow 5} f(x) \)
(A) \(\displaystyle \lim_{x \rightarrow 5^-} f(x) \)
\begin{equation*} \begin{split} \lim_{x \rightarrow 5^-} \frac {x - 5}{x + 1} & = \lim_{x \rightarrow 5^-} \frac {5^- - 5}{5 + 1} \\\\ \lim_{x \rightarrow 5^-} \frac {x - 5}{x + 1} & = \frac {-0}{6} \\\\ \lim_{x \rightarrow 5^-} \frac {x - 5}{x + 1} & = 0 \end{split} \end{equation*}
(B) \(\displaystyle \lim_{x \rightarrow 5^+} f(x) \)
\begin{equation*} \begin{split} \lim_{x \rightarrow 5^+} \frac {x - 5}{x + 1} & = \lim_{x \rightarrow 5^+} \frac {5^+ - 5}{5 + 1} \\\\ \lim_{x \rightarrow 5^+} \frac {x - 5}{x + 1} & = \frac {+0}{6} \\\\ \lim_{x \rightarrow 5^+} \frac {x - 5}{x + 1} & = 0 \end{split} \end{equation*}
(C) \(\displaystyle \lim_{x \rightarrow 5} f(x) \)
\(\displaystyle \lim_{x \rightarrow 5^-} \frac {x - 5}{x + 1} = \lim_{x \rightarrow 5^+} \frac {x - 5}{x + 1} = 0 \)
Contoh 02
Diketahui \(f(x) = \dfrac {x}{x - 2}\)
Tentukan:
(A) \(\displaystyle \lim_{x \rightarrow 2^-} f(x) \)
(B) \(\displaystyle \lim_{x \rightarrow 2^+} f(x) \)
(C) \(\displaystyle \lim_{x \rightarrow 2} f(x) \)
(A) \(\displaystyle \lim_{x \rightarrow 2^-} f(x) \)
\begin{equation*} \begin{split} \lim_{x \rightarrow 2^-} \frac {x}{x - 2} & = \lim_{x \rightarrow 2^-} \frac {2}{2^- - 2} \\\\ \lim_{x \rightarrow 2^-} \frac {x}{x - 2} & = \frac {2}{-0} \\\\ \lim_{x \rightarrow 2^-} \frac {x}{x - 2} & = - \sim \end{split} \end{equation*}
(B) \(\displaystyle \lim_{x \rightarrow 2^+} f(x) \)
\begin{equation*} \begin{split} \lim_{x \rightarrow 2^+} \frac {x}{x - 2} & = \lim_{x \rightarrow 2^+} \frac {2}{2^+ - 2} \\\\ \lim_{x \rightarrow 2^+} \frac {x}{x - 2} & = \frac {2}{+0} \\\\ \lim_{x \rightarrow 2^+} \frac {x}{x - 2} & = + \sim \end{split} \end{equation*}
(C) \(\displaystyle \lim_{x \rightarrow 2} f(x) \)
\(\displaystyle \lim_{x \rightarrow 2^-} \frac {x}{x - 2} \neq \lim_{x \rightarrow 2^+} \frac {x}{x - 2} \)
Maka \(\displaystyle \lim_{x \rightarrow 2} \frac {x}{x - 2} \) tidak ada.
SIFAT-SIFAT LIMIT
Jika \(\displaystyle \lim_{x\to c} f(x) = L\) dan \(\displaystyle \lim_{x\to c} g(x) = M\)
1. Aturan penjumlahan
\(\displaystyle \lim_{x\to c} (f(x) + g(x)) = \lim_{x\to c} f(x) + \lim_{x\to c} g(x) = L + M\)
2. Aturan pengurangan
\(\displaystyle \lim_{x\to c} (f(x) - g(x)) = \lim_{x\to c} f(x) - \lim_{x\to c} g(x) = L - M\)
3. Aturan perkalian konstanta
\(\displaystyle \lim_{x\to c} (k \:.\: f(x)) = k \:.\: \lim_{x\to c} f(x) = k \:.\: L\)
4. Aturan perkalian fungsi
\(\displaystyle \lim_{x\to c} (f(x) \:.\: g(x)) = \lim_{x\to c} f(x) \:.\: \lim_{x\to c} g(x) = L \:.\: M\)
5. Aturan pembagian fungsi
\(\displaystyle \lim_{x\to c} \dfrac {f(x)}{g(x)} = \dfrac {\displaystyle \lim_{x\to c} f(x)}{\displaystyle \lim_{x\to c} g(x)} = \dfrac {L}{M}\)
6. Aturan pangkat
\(\displaystyle \lim_{x\to c} [f(x)]^n = [\lim_{x\to c} f(x)]^n = L^n\)
7. Aturan akar
\(\displaystyle \lim_{x\to c} \sqrt [n] {f(x)} = \sqrt [n] {\lim_{x\to c} f(x)} = \sqrt [n] {L}\)
Jika n bilangan genap dan L bernilai negatif, maka limit tidak ada.
Contoh 01
Diketahui:
\(\displaystyle \lim_{x \rightarrow p} \: f(x)=6\)
\(\displaystyle \lim_{x \rightarrow p} \: g(x)=3\)
\(\displaystyle \lim_{x \rightarrow p} \: g(x)=2\)
Tentukan nilai dari \(\displaystyle \lim_{x \rightarrow p} \left( \dfrac {f(x) \:.\: g(x)}{h(x)} \right)\)
\begin{equation*} \begin{split} & \lim_{x \rightarrow p} \left( \frac {f(x) \:.\: g(x)}{h(x)} \right) \\\\ & \frac {\displaystyle \lim_{x \rightarrow p} \: f(x) \:.\: \displaystyle \lim_{x \rightarrow p} \: g(x)}{\displaystyle \lim_{x \rightarrow p} \: h(x)} \\\\ & \frac {6 \:.\: 3}{2} \\\\ & \bbox[5px, border: 2px solid magenta] {9} \end{split} \end{equation*}
Contoh 02
Diketahui
\(\displaystyle \lim_{x \rightarrow p} \: f(x)=2\)
\(\displaystyle \lim_{x \rightarrow p}\: g(x)=9\)
Tentukan nilai dari \(\displaystyle \lim_{x \rightarrow p} \left(f^2(x)-2\sqrt{g(x)} \right)\)
\begin{equation*} \begin{split} & \lim_{x \rightarrow p} \left(f^2(x)-2\sqrt{g(x)} \right) \\\\ & \lim_{x \rightarrow p} \: f^2(x)-\lim_{x \rightarrow p} \: 2\sqrt{g(x)} \\\\ & \left[\lim_{x \rightarrow p} \: f(x) \right]^2-2\sqrt{\lim_{x \rightarrow p} \: g(x)} \\\\ & 2^2-2\sqrt{9} \\\\ & 4 - 6 \\\\ & \bbox[5px, border: 2px solid magenta] {-2} \end{split} \end{equation*}
B. BENTUK PEMFAKTORAN
Jika \(\displaystyle \lim_{x \rightarrow a} \dfrac {f(x)}{g(x)} = \dfrac {f(a)}{g(a)} = \dfrac 00\)
Hasil \(\dfrac 00\) dapat diselesaikan dengan cara memfaktorkan, dimana faktornya adalah \(x - a\)
\(\displaystyle \lim_{x \rightarrow a} \dfrac {f(x)}{g(x)} = \dfrac {\cancel {(x - a)} F(x)}{\cancel {(x - a)} G(x)} = \dfrac {F(x)}{G(x)} = \dfrac {F(a)}{G(a)}\)
Beberapa rumus yang biasa digunakan:
\(a^2 - b^2 = (a + b)(a - b)\)
\(a^3 + b^3 = (a + b)(a^2 - ab + b^2)\)
\(a^3 - b^3 = (a - b)(a^2 + ab + b^2)\)
Contoh 01
\(\displaystyle \lim_{x \rightarrow 8} \: \dfrac {x - 8}{x^2 - 64}\)
Jika \(x = 8\) disubstitusikan langsung, akan menghasilkan \(\displaystyle \lim_{x \rightarrow 8} \: \dfrac {x - 8}{x^2 - 64} = \dfrac {8 - 8}{8^2 - 64} = \frac 00 \)
Untuk limit x mendekati 8, faktornya adalah \(x - 8\). Maka bentuk di atas dapat diubah menjadi:
\begin{equation*} \begin{split} & \lim_{x \rightarrow 8} \: \frac {x - 8}{x^2 - 64} \\\\ & \lim_{x \rightarrow 8} \: \frac {x - 8}{(x + 8)(x - 8)} \\\\ & \lim_{x \rightarrow 8} \: \frac {\cancel {x - 8}}{(x + 8) \cancel{(x - 8)}} \\\\ & \lim_{x \rightarrow 8} \: \frac {1}{x + 8} \\\\ & \frac {1}{8 + 8} \\\\ & \bbox[5px, border: 2px solid magenta] {\frac {1}{16}} \end{split} \end{equation*}
Contoh 02
\(\displaystyle \lim_{x \rightarrow 2} \dfrac {x^3 + 2x^2 - 7x - 2}{x^3 - 5x^2 + 13x - 14}\)
Apabila x = 2 disubstitusi:
\(\displaystyle \lim_{x \rightarrow 2} \dfrac {(2)^3 + 2(2)^2 - 7(2) - 2}{(2)^3 - 5(2)^2 + 13(2) - 14} = \dfrac 00\)
Maka bentuk polinomial harus difaktorkan terlebih dahulu.
Karena limit x mendekati 2, maka faktornya adalah (x − 2).
\begin{equation*} \begin{split} & \lim_{x \rightarrow 2} \: \frac {x^3 + 2x^2 - 7x - 2}{x^3 - 5x^2 + 13x - 14} \\\\ & \lim_{x \rightarrow 2} \: \frac {(x - 2)(x^2 + 4x + 1)}{(x - 2)(x^2 - 3x + 7)} \\\\ & \lim_{x \rightarrow 2} \: \frac {\cancel{(x - 2)}(x^2 + 4x + 1)}{\cancel{(x - 2)}(x^2 - 3x + 7)} \\\\ & \lim_{x \rightarrow 2} \: \frac {x^2 + 4x + 1}{x^2 - 3x + 7} \\\\ & \frac {(2)^2 + 4 (2) + 1}{(2)^2 - 3 (2) + 7} \\\\ & \bbox[5px, border: 2px solid magenta] {\frac {13}{5}} \end{split} \end{equation*}
Faktorisasi polinomial dapat dilakukan dengan cara pembagian bersusun atau metode Horner.
SELISIH PECAHAN
\(\displaystyle \lim_{x \rightarrow a} \dfrac {1}{f(x)} - \dfrac {1}{g(x)} = \dfrac {1}{f(a)} - \dfrac {1}{g(a)} = \dfrac 10 - \dfrac 10 = \: \sim - \sim\)
Hasil \(\: \sim - \sim\) dapat diselesaikan dengan cara memfaktorkan \(f(x)\) dan \(g(x)\), dimana faktornya adalah \(x - a\)
\(\displaystyle \lim_{x \rightarrow a} \dfrac {1}{(x - a) \:.\: F(x)} - \dfrac {1}{(x - a) \:.\: G(x)} = \dfrac {G(x) - F(x)}{(x - a) \:.\: F(x) \:.\: G(x)}\)
Contoh 03
\(\displaystyle \lim_{x \rightarrow -3} \left(\frac{6}{x^2-9}-\frac{1}{x^2+5x+6}\right)\)
Jika \(x = -3\) disubstitusikan langsung, akan menghasilkan:
\(\displaystyle \lim_{x \rightarrow -3} \: \left(\frac{6}{x^2-9}-\frac{1}{x^2+5x+6}\right) = \frac{6}{(-3)^2-9}-\frac{1}{(-3)^2+5(-3)+6} = \frac 60 - \frac 10 = \: \sim - \sim\)
Untuk limit x mendekati −3, faktornya adalah \(x + 3\). Maka bentuk di atas dapat diubah menjadi:
\begin{equation*} \begin{split} & \lim_{x \rightarrow -3} \: \left(\frac{6}{x^2-9}-\frac{1}{x^2+5x+6} \right) \\\\ & \lim_{x \rightarrow -3} \: \left(\frac{6}{(x + 3)(x - 3)}-\frac{1}{(x + 3)(x + 2)} \right) \\\\ & \lim_{x \rightarrow -3} \: \frac{6(x + 2) - (x - 3)}{(x + 3)(x - 3)(x + 2)} \\\\ & \lim_{x \rightarrow -3} \: \frac{6x + 12 - x + 3}{(x + 3)(x - 3)(x + 2)} \\\\ & \lim_{x \rightarrow -3} \: \frac{5x + 15}{(x + 3)(x - 3)(x + 2)} \\\\ & \lim_{x \rightarrow -3} \: \frac{5(x + 3)}{(x + 3)(x - 3)(x + 2)} \\\\ & \lim_{x \rightarrow -3} \: \frac{5 \cancel {(x + 3)}}{\cancel {(x + 3)}(x - 3)(x + 2)} \\\\ & \lim_{x \rightarrow -3} \: \frac{5}{(x - 3)(x + 2)} \\\\ & \frac{5}{(-3 - 3)(-3 + 2)} \\\\ & \frac {5}{-6 \:.\: -1} \\\\ & \bbox[5px, border: 2px solid magenta] {\frac{5}{6}} \end{split} \end{equation*}
C. KALI SEKAWAN
\(\displaystyle \lim_{x \rightarrow a} \dfrac {1}{\sqrt{x + m} - \sqrt{x + n}} \times \dfrac {\sqrt{x + m} + \sqrt{x + n}}{\sqrt{x + m} + \sqrt{x + n}} = \dfrac {\sqrt{x + m} + \sqrt{x + n}}{(x + m) - (x + n)}\)
Penjelasan
\((a + b)(a - b) = a^2 - b^2\)
\((\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b}) = (\sqrt{a})^2 - (\sqrt{b})^2 = a - b\)
\((\sqrt{x + m} + \sqrt{x + n})(\sqrt{x + m} - \sqrt{x + n}) = (\sqrt{x + m})^2 - (\sqrt{x + n})^2 = (x + m) - (x + n)\)
[/dt_sc_titled_box]
Contoh
\begin{equation*} \begin{split} & \lim_{x \rightarrow 0} \: \frac{2 - \sqrt{4 - x}}{x} \\\\ & \lim_{x \rightarrow 0} \: \frac{2 - \sqrt{4 - x}}{x} {\color {blue} \times \frac {2 + \sqrt{4 - x}}{2 + \sqrt{4 - x}}}\\\\ & \lim_{x \rightarrow 0} \: \frac{4 - (4 - x)}{x (2 + \sqrt{4 - x})} \\\\ & \lim_{x \rightarrow 0} \: \frac{4 - 4 + x}{x (2 + \sqrt{4 - x})} \\\\ & \lim_{x \rightarrow 0} \: \frac{\cancel{x}}{\cancel{x} (2 + \sqrt{4 - x})} \\\\ & \lim_{x \rightarrow 0} \: \frac{1}{2 + \sqrt{4 - x}} \\\\ & \frac{1}{2 + \sqrt{4 - 0}} \\\\ & \frac {1}{2 + 2} \\\\ & \bbox[5px, border: 2px solid magenta] {\frac 14} \end{split} \end{equation*}
D. ATURAN L'HOPITAL
Aturan L'Hopital dapat digunakan apabila:
\(\displaystyle \lim_{x \rightarrow a} \dfrac {f(x)}{g(x)} = \dfrac {f(a)}{g(a)} = \dfrac 00\) atau \(\dfrac {\sim}{\sim}\)
Aturan L'Hopital:
\(\displaystyle \lim_{x \rightarrow a} \dfrac {f(x)}{g(x)} = \lim_{x \rightarrow a} \dfrac {f'(x)}{g'(x)}\)
dimana \(f'(x)\) dan \(g'(x)\) adalah turunan pertama dari \(f(x)\) dan \(g(x)\)
Contoh
\(\displaystyle \lim_{x \rightarrow 5} \dfrac {x^2 - 25}{x - 5}\)
Bila kita substitusikan \(x = 5\) ke dalam \(\dfrac {x^2 - 25}{x - 5}\) akan menghasilkan \(\dfrac {5^2 - 25}{5 - 5} = \dfrac 00\)
Dengan menggunakan aturan L'Hopital, \(\displaystyle \lim_{x \rightarrow 5} \dfrac {x^2 - 25}{x - 5} = \dfrac {2x}{1} = 2(5) = 10\)
E. LIMIT TAK HINGGA
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac {ax^m + \dotso}{bx^n + \dotso}\)
Limit x mendekati tak terhingga diselesaikan dengan cara membagi pembilang dan penyebut dengan pangkat terbesar.
Bentuk 1 (m = n)
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac {ax^m + \dotso}{bx^m + \dotso} = \dfrac ab\)
Bentuk 2 (m > n)
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac {ax^m + \dotso}{bx^n + \dotso} = \: \sim\)
Bentuk 3 (m < n)
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac {ax^m + \dotso}{bx^n + \dotso} = 0\)
Hasil akhir hanya ditentukan oleh suku dengan pangkat terbesar saja. Suku-suku lainnya akan bernilai 0.
Bentuk 1 (m = n)
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac {ax^m + \dotso}{bx^n + \dotso} = \dfrac ab\)
Contoh:
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac{6x^3-2x^2-1}{2x^3-8x^2+4}\)
Variabel dengan pangkat terbesar adalah \(x^3\). Maka pembilang dan penyebut dibagi dengan \(x^3\).
\begin{equation*} \begin{split} & \lim_{x \rightarrow \sim} \: \dfrac{6x^3-2x^2-1}{2x^3-8x^2+4} \\\\ & \lim_{x \rightarrow \sim} \: \dfrac{6x^3-2x^2-1}{2x^3-8x^2+4} {\color {blue} \times \frac {\dfrac {1}{x^3}}{\dfrac {1}{x^3}}} \\\\ & \lim_{x \rightarrow \sim} \: \frac {6 - \dfrac {2}{x} - \dfrac {1}{x^3}}{2 - \dfrac {8}{x} + \dfrac {4}{x^3}} \\\\ & \frac {6 - \dfrac {2}{\sim} \: - \dfrac {1}{\sim}}{2 - \dfrac {8}{\sim} + \dfrac {4}{\sim}} \\\\ & \frac {6 - 0 - 0}{2 - 0 + 0} \\\\ & \frac 62 \\\\ & \bbox[5px, border: 2px solid magenta] {3} \end{split} \end{equation*}
Bentuk 2 (m > n)
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac {ax^m + \dotso}{bx^n + \dotso} = \: \sim\)
Contoh:
\(\displaystyle \lim_{x \rightarrow \sim}\frac{2x^5-x^3-8}{4x^3-x}\)
Variabel dengan pangkat terbesar adalah \(x^5\). Maka pembilang dan penyebut dibagi dengan \(x^5\).
\begin{equation*} \begin{split} & \lim_{x \rightarrow \sim} \: \frac{2x^5-x^3-8}{4x^3-x} \\\\ & \lim_{x \rightarrow \sim} \: \frac{2x^5-x^3-8}{4x^3-x} {\color {blue} \times \frac {\dfrac {1}{x^5}}{\dfrac {1}{x^5}}} \\\\ & \lim_{x \rightarrow \sim} \: \frac {2 - \dfrac {1}{x^2} - \dfrac {8}{x^5}}{\dfrac {4}{x^2} - \dfrac {1}{x^4}} \\\\ & \frac {2 - \dfrac {1}{\sim} \: - \dfrac {8}{\sim}}{\dfrac {4}{\sim} - \dfrac {1}{\sim}} \\\\ & \frac {2 - 0 - 0}{0 - 0} \\\\ & \frac 20 \\\\ & \bbox[5px, border: 2px solid magenta] {\: \sim} \end{split} \end{equation*}
Bentuk 3 (m < n)
\(\displaystyle \lim_{x \rightarrow \sim} \: \dfrac {ax^m + \dotso}{bx^n + \dotso} = 0\)
Contoh:
\(\displaystyle \lim_{x \rightarrow \sim} \: \frac{2x^5-4x^3-7}{2x^8-8x^3+3}\)
Variabel dengan pangkat terbesar adalah \(x^8\). Maka pembilang dan penyebut dibagi dengan \(x^8\).
\begin{equation*} \begin{split} & \lim_{x \rightarrow \sim} \: \frac{2x^5-4x^3-7}{2x^8-8x^3+3} \\\\ & \lim_{x \rightarrow \sim} \: \frac{2x^5-4x^3-7}{2x^8-8x^3+3} {\color {blue} \times \frac {\dfrac {1}{x^8}}{\dfrac {1}{x^8}}} \\\\ & \lim_{x \rightarrow \sim} \: \frac {\dfrac{2}{x^3} - \dfrac {4}{x^5} - \dfrac {7}{x^8}}{2 - \dfrac {8}{x^5} + \dfrac {3}{x^8}} \\\\ & \frac {\dfrac{2}{\sim} \: - \dfrac {4}{\sim} - \dfrac {7}{\sim}}{2 - \dfrac {8}{\sim} + \dfrac {3}{\sim}} \\\\ & \frac {0 - 0 - 0}{2 - 0 + 0} \\\\ & \frac 02 \\\\ & \bbox[5px, border: 2px solid magenta] {0} \end{split} \end{equation*}
Pada ketiga contoh soal di atas, dapat dilihat bahwa hasil akhir hanya ditentukan oleh suku dengan pangkat terbesar saja. Suku-suku lainnya akan bernilai 0.
F. KONTINUITAS FUNGSI
Sebuah fungsi \(f(x)\) kontinu pada x = a jika memenuhi syarat:
(1) \(f(a)\) terdefinisi
(2) \(\displaystyle \lim_{x \rightarrow a^-} f(x)\) terdefinisi
(3) \(\displaystyle \lim_{x \rightarrow a^+} f(x)\) terdefinisi
(4) \(f(a) = \displaystyle \lim_{x \rightarrow a^-} f(x) =\displaystyle \lim_{x \rightarrow a^+} f(x)\)
[/dt_sc_titled_box]
Sebuah fungsi disebut kontinu pada interval tertentu apabila pada setiap titik dalam interval tersebut, kurva fungsi tidak terputus.
Fungsi kontinu

Fungsi diskontinu pada x = 2

Contoh
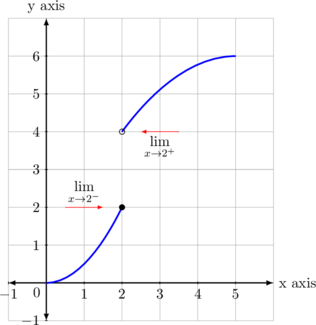
\(f(2) = 2\)
\(\displaystyle \lim_{x \rightarrow 2^-} f(x) = 2\)
\(\displaystyle \lim_{x \rightarrow 2^+} f(x) = 4\)
Karena \(\displaystyle \lim_{x \rightarrow 2^-} f(x) \neq \lim_{x \rightarrow 2^+} f(x)\) maka fungsi diskontinu pada x = 2
