A. PERSAMAAN LINGKARAN
1. Lingkaran Dengan Pusat (0,0)

\(x^2 + y^2 = R^2\)
Pusat lingkaran (0,0)
Radius lingkaran R
2. Lingkaran Dengan Pusat (a,b)

\((x - a)^2 + (y - b)^2 = R^2\)
Pusat lingkaran (a,b)
Radius lingkaran R
3. Persamaan Lingkaran Bentuk Umum

\(x^2 + y^2 + Ax + By + C = 0\)
Pusat lingkaran \(\left(-\dfrac{1}{2}A,-\dfrac{1}{2}B \right)\)
Radius lingkaran \(R = \sqrt{\dfrac 14 A^2 + \dfrac 14 B^2 - C}\)
B. TITIK, GARIS DAN LINGKARAN
Titik Kuasa Dan Garis Kuasa
1. Kuasa titik M \((x_1,y_1)\) terhadap lingkaran \(x^2 + y^2 + Ax + By + C = 0\)
\(K = x_1^2 + y_1^2 + Ax_1 + By_1 + C\)
- \(K < 0\) → titik M berada di dalam lingkaran
- \(K = 0\) → titik M berada tepat pada lingkaran
- \(K > 0\) → titik M berada di luar lingkaran
2. Garis Kuasa Dua Lingkaran
Persamaan garis kuasa dari dua lingkaran \(L_1\) dan \(L_2\) adalah:
\(L_1 - L_2 = 0\)
3. Titik Kuasa Tiga Lingkaran
Titik kuasa dari lingkaran \(L_1\), \(L_2\) dan \(L_3\) adalah titik perpotongan dari tiga garis kuasa, yaitu garis kuasa dari \(L_1\) dan \(L_2\), garis kuasa dari \(L_1\) dan \(L_3\) dan garis kuasa dari \(L_2\) dan \(L_3\).
Hubungan Titik, Garis Dan Lingkaran
1. Jarak Titik Dan Lingkaran
Jarak titik M ke lingkaran untuk titik M yang berada di luar lingkaran:
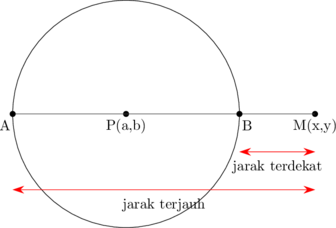
Jarak terdekat = jarak BM
AM = jarak PM − PB
AM = jarak titik P ke titik M − radius lingkaran
AM = \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} - R\)
Jarak terjauh = jarak AM
AM = jarak AP + PM
AM = radius lingkaran + jarak titik P ke titik M
AM = \(R + \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
2. Hubungan Garis Dan Lingkaran
Dengan mensubstitusikan persamaan garis \(y = mx + c\) ke persamaan lingkaran \(x^2 + y^2 + Ax + By + C = 0\), dan menentukan nilai Diskriminan (D), didapat hubungan antara garis dan lingkaran.
\(D = b^2 - 4ac\)
- Jika \(D < 0\) → garis tidak memotong lingkaran
- Jika \(D = 0\) → garis menyinggung lingkaran
- Jika \(D > 0\) → garis memotong lingkaran di 2 titik berbeda
3. Hubungan 2 Lingkaran
Hubungan antara 2 lingkaran didapat dengan cara membandingkan jarak antara titik pusat kedua lingkaran dan jari-jari kedua lingkaran.
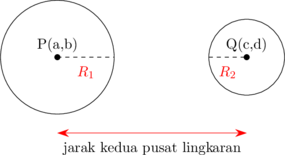
\(PQ > R_1 + R_2\)
Kedua lingkaran terpisah
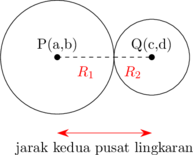
\(PQ = R_1 + R_2\)
Kedua lingkaran bersinggungan luar
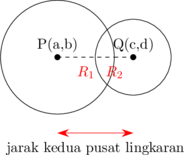
\(PQ < R_1 + R_2\)
Kedua lingkaran berpotongan
C. GARIS SINGGUNG DAN GARIS POLAR
Garis Singgung Lingkaran
1. Diketahui titik \((x_1,y_1)\) pada lingkaran
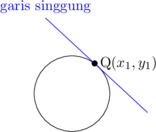
| Lingkaran | Garis Singgung |
| \(x^2 + y^2 = R^2\) | \(x_1 \: x + y_1 \: y = R^2\) |
| \((x - a)^2 + (y - b)^2 = R^2\) | \((x_1 - a)(x - a) + (y_1 - b)(y - b) = R^2\) |
| \(x^2 + y^2 + Ax + By + C = 0\) | \(x_1 \: x + y_1 \: y + \dfrac{1}{2}A(x + x_1) + \dfrac{1}{2}B(y + y_1) + C = 0\) |
2. Diketahui Titik Di Luar Lingkaran
-
- Tentukan persamaan garis polar
- Tentukan titik potong garis polar dan lingkaran
- Tentukan persamaan garis singgung (terdapat 2 garis singgung)
3. Diketahui Gradien Garis Singgung
-
- \(y - b = m(x - a) \pm R \sqrt{1 + m^2}\)
- \((a,b)\) adalah pusat lingkaran dan R adalah jari-jari lingkaran
- terdapat 2 garis singgung
Garis Polar
Garis polar dari sebuah lingkaran yang ditarik dari titik M (\(x_1,y_1)\)
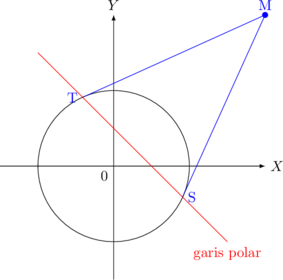
| Lingkaran | Garis Polar |
| \(x^2 + y^2 = R^2\) | \(x_1 \: x + y_1 \: y = R^2\) |
| \((x - a)^2 + (y - b)^2 = R^2\) | \((x_1 - a)(x - a) + (y_1 - b)(y - b) = R^2\) |
| \(x^2 + y^2 + Ax + By + C = 0\) | \(x_1 \: x + y_1 \: y + \dfrac{1}{2}A(x + x_1) + \dfrac{1}{2}B(y + y_1) + C = 0\) |
D. BERKAS LINGKARAN
Persamaan berkas lingkaran yang dibentuk dari lingkaran \(L_1\) dan \(L_2\)
\(L_1 + \lambda \:.\: L_2 = 0\)
\(\lambda\) adalah konstanta
