A. NILAI EFEKTIF
| Tegangan | Arus | |
|---|---|---|
| Nilai Sesaat | \(V = V_{\text{max}} \:.\: \sin \omega t\) | \(I = I_{\text{max}} \:.\: \sin \omega t\) |
| Nilai Efektif | \(V_{\text{eff}} = \dfrac {V_{\text{max}}}{\sqrt{2}}\) | \(I_{\text{eff}} = \dfrac {I_{\text{max}}}{\sqrt{2}}\) |
| Nilai Rata-rata | \(V_{\text{rata-rata}} = \dfrac {2 \:.\: V_{\text{max}}}{\pi}\) | \(I_{\text{rata-rata}} = \dfrac {2 \:.\: I_{\text{max}}}{\pi}\) |
B. RESISTOR, INDUKTOR DAN KAPASITOR
Resistor
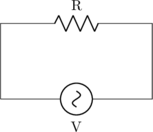
\(V = I \:.\: R\)
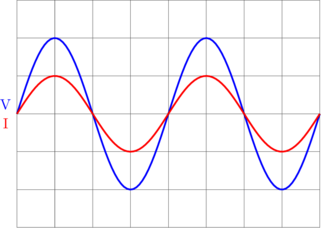
\(V\) dan \(I\) sefase.
\(V = V_{\text{max}} \sin \omega t\)
\(I = I_{\text{max}} \sin \omega t\)
Induktor
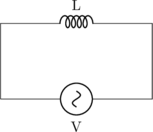
\(V = I \:.\: X_L\)
\(X_L = \omega \:.\: L\)
\(V\) mendahului \(I\).
\(V = V_{\text{max}} \sin \omega t\)
\(I = I_{\text{max}} \sin (\omega t - 90)\)
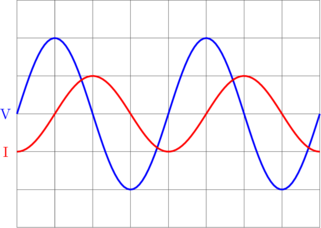
\(V = V_{\text{max}} \sin (\omega t + 90)\)
\(I = I_{\text{max}} \sin \omega t\)
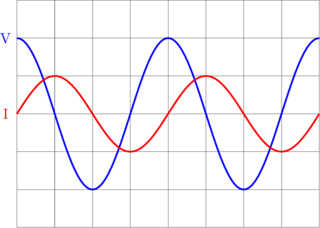
Kapasitor
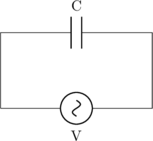
\(V = I \:.\: X_C\)
\(X_L = \dfrac {1}{\omega \:.\: C}\)
\(I\) mendahului \(V\).
\(V = V_{\text{max}} \sin \omega t\)
\(I = I_{\text{max}} \sin (\omega t + 90)\)

\(V = V_{\text{max}} \sin (\omega t - 90)\)
\(I = I_{\text{max}} \sin \omega t\)
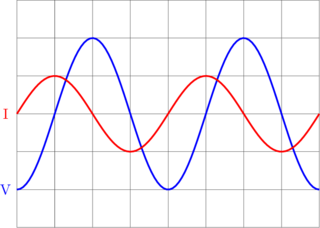
C. RANGKAIAN RLC
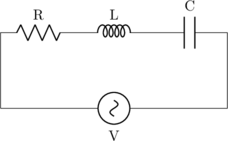
Impedansi
\(Z = \sqrt{R^2 + (X_L - X_C)^2}\)
Tegangan dan kuat arus
\(V = I \:.\: Z\)
\(V_R = I \:.\: R\)
\(V_L = I \:.\: X_L\)
\(V_C = I \:.\: X_C\)
\(V = \sqrt{V_R^2 + (V_L - V_C)^2}\)
Beda fase tegangan dan arus
\(\tan \theta = \dfrac {X_L - X_C}{R}\)
\(\tan \theta = \dfrac {V_L - V_C}{V_R}\)
Daya
\(P_{\text{eff}} = V_{\text{eff}} \:.\: I_{\text{eff}} \:.\: \cos \theta\)
\(P_{\text{eff}} = I_{\text{eff}}^2 \:.\: R\)
Faktor daya
\(\cos \theta = \dfrac {R}{Z} = \dfrac {V_R}{V}\)
Resonansi
Resonansi terjadi saat reaktansi induktif \(X_L\) sama besar dengan reaktansi kapasitif \(X_C\).
\(X_L = X_C\)
Frekuensi resonansi
\begin{equation*} \begin{split} X_L & = X_C \\\\ \omega \:.\: L & = \frac {1}{\omega \:.\: C} \\\\ \omega^2 & = \frac {1}{LC} \\\\ \omega & = \sqrt{\frac {1}{LC}} \\\\ 2 \pi \:.\: f & = \frac {1}{\sqrt{LC}} \\\\ f & = \frac {1}{2 \pi \sqrt{LC}} \end{split} \end{equation*}
Saat terjadi resonansi, nilai impedanzi \(Z\) mencapai minimum dan kuat arus \(I\) mencapai maksimum.
A. Nilai Efektif B. Resistor, Induktor dan Kapasitor C. Rangkaian RLC D. Persiapan Ulangan Kembali ke Modul SMA
