A. GAYA ELEKTROSTATIK
Gaya elektrostatis adalah gaya tarik-menarik atau tolak-menolak antara dua buah muatan.
Muatan berlawanan jenis akan tarik menarik

Muatan sejenis akan tolak menolak

Muatan sejenis akan tolak menolak

Besar Gaya Elektrostatik
Gaya Elektrostatik Dalam Hampa Udara
\begin{equation*} \begin{split} & \bbox[10px, border: 2px solid red]{F = \frac{1}{4 \pi \varepsilon_o} \:.\: \frac{Q_1 \:.\: Q_2}{r^2} = k \:.\: \frac{Q_1 \:.\: Q_2}{r^2}} \\\\ & k = \frac{1}{4 \pi \varepsilon_o} = 9 \times 10^9 \\\\ & \varepsilon_o = 8,85 \times 10^{-12} \text{ (permitivitas hampa udara)} \end{split} \end{equation*}
Gaya Elektrostatik Dalam Bahan
\begin{equation*} \begin{split} & \bbox[10px, border: 2px solid red]{F_{\text{bahan}} = \frac{1}{4 \pi \varepsilon_r \:.\: \varepsilon_o} \:.\: \frac{Q_1 \:.\: Q_2}{r^2} = \frac{k}{\varepsilon_r} \:.\: \frac{Q_1 \:.\: Q_2}{r^2}} \\\\ & F_{\text{bahan}} = \frac{F_{\text{hampa udara}}}{\varepsilon_r} \\\\ & \varepsilon_r = \text{permitivitas relatif bahan } (\varepsilon_r > 1) \end{split} \end{equation*}
Karena \(\varepsilon_r > 1\), maka gaya elektrostatis di dalam bahan lebih kecil daripada gaya elektrostatis di dalam hampa udara.
B. MEDAN LISTRIK
Medan listrik adalah daerah di sekeliling muatan yang masih dipengaruhi oleh muatan tersebut.
Medan listrik oleh muatan positif mengarah ke luar

Medan listrik oleh muatan positif mengarah ke dalam

1. Kuat medan listrik suatu titik berjarak r dari muatan

\(\bbox[10px, border: 2px solid red]{E = k \:.\: \dfrac{Q}{r^2}}\)

\(\bbox[10px, border: 2px solid red]{E = k \:.\: \dfrac{Q}{r^2}}\)
2. Muatan di dalam medan listrik
Muatan positif di dalam medan listrik
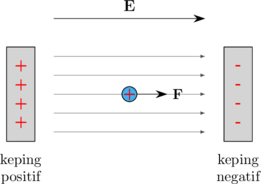
\(\bbox[10px, border: 2px solid red]{F = q \:.\: E}\)
Arah gaya elektrostatik pada muatan positif searah dengan arah medan listrik
Muatan negatif di dalam medan listrik
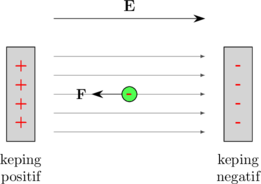
\(\bbox[10px, border: 2px solid red]{F = q \:.\: E}\)
Arah gaya elektrostatik pada muatan negatif berlawanan dengan arah medan listrik
3. Fluks Listrik
Fluks listrik adalah jumlah medan listrik yang berada dalam luas tertentu.
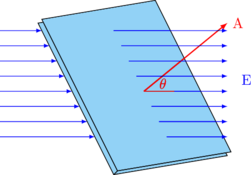
\begin{equation*} \begin{split} & \Theta = E \cdot A \\\\ & \bbox[10px, border: 2px solid red]{\Theta = E \:.\: A \:.\: \cos \theta} \end{split} \end{equation*}
C. POTENSIAL DAN ENERGI LISTRIK
1. Potensial Listrik oleh Muatan
Potensial listrik sebuah titik pada jarak \(r\) dari sebuah muatan:

\(\bbox[10px, border: 2px solid red]{V = k \:.\: \dfrac{Q}{r}}\)
2. Beda Potensial Listrik Antara Dua Titik
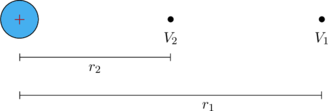
\(\bbox[10px, border: 2px solid red]{\Delta V = V_2 - V_1}\)
\(\Delta V = k \:.\: \dfrac{Q}{r_2} - k \: \dfrac{Q}{r_1}\)
\(\Delta V = k \:.\: Q \left(\dfrac{1}{r_2} - \dfrac{1}{r_1}\right)\)
Titik dengan potensial lebih tinggi ditandai dengan (+) dan titik dengan potensial lebih rendah ditandai dengan (−)
3. Beda Potensial pada Medan Listrik

\(\bbox[10px, border: 2px solid red]{\Delta V = E \:.\: d}\)
4. Energi Potensial Listrik Pada Dua Muatan
\(\bbox[10px, border: 2px solid red]{E_p = k \:.\: \dfrac{q \:.\: Q}{r}} \)
5. Usaha
Besar usaha yang diperlukan untuk memindahkan muatan dari satu titik ke titik lainnya:
\begin{equation*} \begin{split} & W = \Delta E_p \\\\ & W = E_{p_2} - E_{p_1} \\\\ & W = q \:.\: V_2 - q \:.\: V_1 \\\\ & W = q \:.\: (V_2 - V_1) \\\\ & \bbox[10px, border: 2px solid red]{W = q \:.\: \Delta V} \end{split} \end{equation*}
D. BOLA KONDUKTOR
Bila sebuah logam berbentuk bola diberi muatan, maka muatan akan berada di bagian permukaan dalam bola.

Kuat medan listrik dan potensial listrik oleh bola konduktor bermuatan Q dengan jari-jari R
| Posisi | E | V |
|---|---|---|
| Di dalam bola | 0 | \(k \: \dfrac{Q}{R}\) |
| Di permukaan bola | \(k \: \dfrac{Q}{R^2}\) | \(k \: \dfrac{Q}{R}\) |
| Di luar bola pada jarak \(r\) | \(k \: \dfrac{Q}{r^2}\) | \(k \: \dfrac{Q}{r}\) |
