SOAL 01
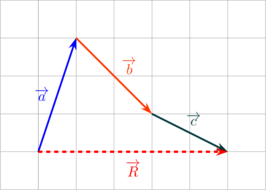
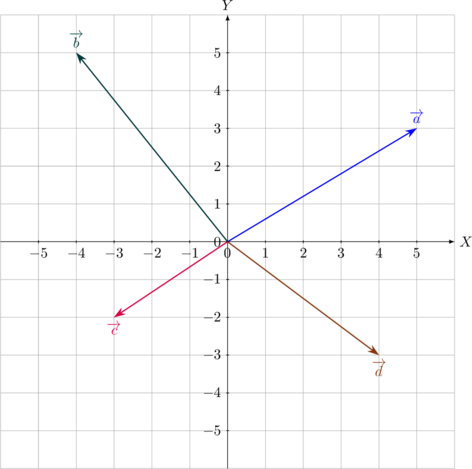
Diketahui tiga buah vektor seperti gambar di bawah ini.
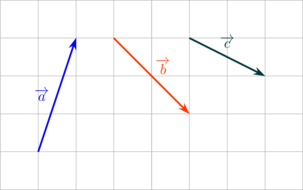
Tentukan:
(A) \(\overrightarrow R = \overrightarrow a + \overrightarrow b + \overrightarrow c\)
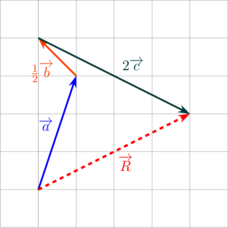
(B) \(\overrightarrow R = \overrightarrow a - \frac 12 \overrightarrow b + 2 \overrightarrow c\)
SOAL 02
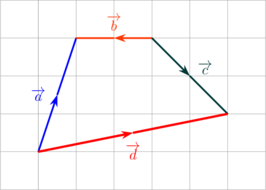
Pada gambar di bawah ini, tentukan \(\overrightarrow a\) dalam \(\overrightarrow b\), \(\overrightarrow c\) dan \(\overrightarrow d\)
SOAL 03
Seorang anak melakukan perjalanan sebagai berikut:
-
- Berjalan sejauh 40 m dengan arah 53º utara dari timur
- Berjalan sejauh 30 m ke arah timur
- Berjalan sejauh 50 m ke arah selatan
Gambarkan perjalanan anak tersebut dan tentukan besar dan arah resultannya.
SOAL 04
Sebuah kapal berlayar sejauh 10 km pada arah JTA 030, kemudian berbelok ke arah JTA 315 sejauh 8 km dan kemudian ke arah 270 sejauh 8 km.
Gambarkan perjalanan kapal dengan metode poligon dan perpindahan kapal dari awal berangkat hingga tujuan akhir.
SOAL 05
Sebuah motor-boat ingin menyeberangi sungai yang lebarnya 1200 m. Perahu diarahkan tegak lurus arah arus.

Aliran sungai deras dengan kecepatan 7 m/s. Jika kecepatan perahu pada air yang tenang 24 m/s, tentukan:
(A) Resultan kecepatan perahu
(B) Waktu yang dibutuhkan perahu untuk menyeberang
(C) Jika motor-boat tiba di titik R, tentukan jarak QR
(D) Kemanakah perahu harus diarahkan agar perahu tiba tepat di seberang posisinya semula? (sudut dihitung dari arah motor-boat mula-mula)
SOAL 06
Dua buah vektor gaya besarnya masing-masing \(F_1 = 6\) satuan dan \(F_2 = 3\) satuan, saling membentuk sudut 60°. Tentukan:
(A) Besar resultan \(R\)
(B) Sudut antara resultan dan \(F_1\)
(C) Sudut antara resultan dan \(F_2\)
SOAL 07
Dua buah vektor yang besarnya sama membentuk sudut θ. Jika resultan kedua vektor sama dengan selisih kedua vektor tersebut, tentukan besar θ.
SOAL 08
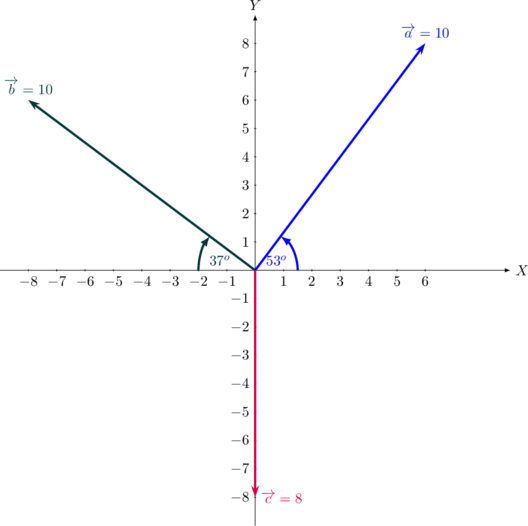
Tentukan resultan vektor-vektor di bawah ini dengan metode komponen vektor:
1 kotak = 1 satuan
SOAL 09
Tentukan resultan vektor-vektor di bawah ini:
SOAL 10
SOAL 11
SOAL 12
SOAL 13