Perbandingan Trigonometri

25 Dec

Perbandingan Trigonometri

Andidj

off

TRIGONOMETRI

A. Segitiga Siku-siku

Rendered by QuickLaTeX.com

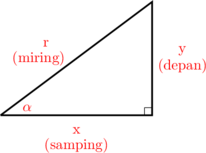
\(\sin \alpha = \dfrac yr = \dfrac {\text{depan}}{\text{miring}}\)

\(\cos \alpha = \dfrac xr = \dfrac {\text{samping}}{\text{miring}}\)

\(\tan \alpha = \dfrac yx = \dfrac {\text{depan}}{\text{samping}}\)

\(\sec \alpha = \dfrac {1}{\cos \alpha} \)

\(\csc \alpha = \dfrac {1}{\sin \alpha} \)

\(\cot \alpha = \dfrac {1}{\tan \alpha} \)

Sudut Istimewa

	\(0\)	\(30^{\text{o}}\)	\(45^{\text{o}}\)	\(60^{\text{o}}\)	\(90^{\text{o}}\)	\(37^{\text{o}}\)	\(53^{\text{o}}\)
Sin	0	\(\dfrac{1}{2}\)	\(\dfrac{1}{2}\sqrt{2}\)	\(\dfrac{1}{2}\sqrt{3}\)	1	\(0,6\)	\(0,8\)
Cos	1	\(\dfrac{1}{2}\sqrt{3}\)	\(\dfrac{1}{2}\sqrt{2}\)	\(\dfrac{1}{2}\)	0	\(0,8\)	\(0,6\)
Tan	0	\(\dfrac{1}{3} \sqrt{3}\)	1	\(\sqrt{3}\)	∼	\(\dfrac 34\)	\(\dfrac 43\)

B. RELASI SUDUT

1. Kuadran

Rendered by QuickLaTeX.com

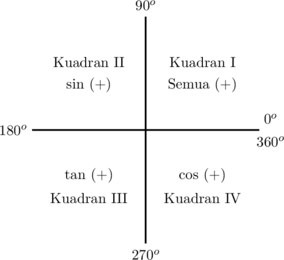
2. Sudut di kuadran II (\(90^\text{o} < \alpha < 180^\text{o}\))

Menggunakan \((180^\text{o} - \alpha)\)	Menggunakan \((90^\text{o} + \alpha)\)
\begin{equation} \begin{split} & \sin 150^\text{o} = \sin (180^\text{o} - 30^\text{o}) \\\\ & \sin 150^\text{o} = + \sin 30^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 150^\text{o} = + \tfrac 12} \end{split} \end{equation} 150º berada di kuadran II, maka sin 150º bernilai positif.	\begin{equation} \begin{split} & \sin 150^\text{o} = \sin (90^\text{o} + 60^\text{o}) \\\\ & \sin 150^\text{o} = + \cos 60^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 150^\text{o} = + \tfrac 12} \end{split} \end{equation} 150º berada di kuadran II, maka sin 150º bernilai positif.
\begin{equation} \begin{split} & \cos 150^\text{o} = \cos (180^\text{o} - 30^\text{o}) \\\\ & \cos 150^\text{o} = - \cos 30^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\cos 150^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation} 150º berada di kuadran II, maka cos 150º bernilai negatif.	\begin{equation} \begin{split} & \cos 150^\text{o} = \cos (90^\text{o} + 60^\text{o}) \\\\ & \cos 150^\text{o} = - \sin 60^\text{o} \quad {\color {blue} \cos \rightarrow \sin}\\\\ & \bbox[5px, border: 2px solid magenta]{\cos 150^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation} 150º berada di kuadran II, maka cos 150º bernilai negatif.
\begin{equation} \begin{split} & \tan 150^\text{o} = \tan (180^\text{o} - 30^\text{o}) \\\\ & \tan 150^\text{o} = - \tan 30^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\tan 150^\text{o} = - \tfrac 13 \sqrt{3}} \end{split} \end{equation} 150º berada di kuadran II, maka tan 150º bernilai negatif.	\begin{equation} \begin{split} & \tan 150^\text{o} = \tan (90^\text{o} + 60^\text{o}) \\\\ & \tan 150^\text{o} = - \cot 60^\text{o} \quad {\color {blue} \tan \rightarrow \cot}\\\\ & \bbox[5px, border: 2px solid magenta]{\tan 150^\text{o} = - \tfrac 13 \sqrt{3}} \end{split} \end{equation} 150º berada di kuadran II, maka tan 150º bernilai negatif.
\begin{equation} \begin{split} & \sin 180^\text{o} = \sin (180^\text{o} - 0^\text{o}) \\\\ & \sin 180^\text{o} = \sin 0^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 180^\text{o} = 0} \end{split} \end{equation}	\begin{equation} \begin{split} & \sin 180^\text{o} = \sin (90^\text{o} + 90^\text{o}) \\\\ & \sin 180^\text{o} = \cos 90^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 180^\text{o} = 0} \end{split} \end{equation}

Menggunakan \((180^\text{o} - \alpha)\)

Menggunakan \((90^\text{o} + \alpha)\)

\begin{equation*} \begin{split} & \sin 150^\text{o} = \sin (180^\text{o} - 30^\text{o}) \\\\ & \sin 150^\text{o} = + \sin 30^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 150^\text{o} = + \tfrac 12} \end{split} \end{equation*}

150º berada di kuadran II, maka sin 150º bernilai positif.

\begin{equation*} \begin{split} & \sin 150^\text{o} = \sin (90^\text{o} + 60^\text{o}) \\\\ & \sin 150^\text{o} = + \cos 60^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 150^\text{o} = + \tfrac 12} \end{split} \end{equation*}

150º berada di kuadran II, maka sin 150º bernilai positif.

\begin{equation*} \begin{split} & \cos 150^\text{o} = \cos (180^\text{o} - 30^\text{o}) \\\\ & \cos 150^\text{o} = - \cos 30^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\cos 150^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation*}

150º berada di kuadran II, maka cos 150º bernilai negatif.

\begin{equation*} \begin{split} & \cos 150^\text{o} = \cos (90^\text{o} + 60^\text{o}) \\\\ & \cos 150^\text{o} = - \sin 60^\text{o} \quad {\color {blue} \cos \rightarrow \sin}\\\\ & \bbox[5px, border: 2px solid magenta]{\cos 150^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation*}

150º berada di kuadran II, maka cos 150º bernilai negatif.

\begin{equation*} \begin{split} & \tan 150^\text{o} = \tan (180^\text{o} - 30^\text{o}) \\\\ & \tan 150^\text{o} = - \tan 30^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\tan 150^\text{o} = - \tfrac 13 \sqrt{3}} \end{split} \end{equation*}

150º berada di kuadran II, maka tan 150º bernilai negatif.

\begin{equation*} \begin{split} & \tan 150^\text{o} = \tan (90^\text{o} + 60^\text{o}) \\\\ & \tan 150^\text{o} = - \cot 60^\text{o} \quad {\color {blue} \tan \rightarrow \cot}\\\\ & \bbox[5px, border: 2px solid magenta]{\tan 150^\text{o} = - \tfrac 13 \sqrt{3}} \end{split} \end{equation*}

150º berada di kuadran II, maka tan 150º bernilai negatif.

\begin{equation*} \begin{split} & \sin 180^\text{o} = \sin (180^\text{o} - 0^\text{o}) \\\\ & \sin 180^\text{o} = \sin 0^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 180^\text{o} = 0} \end{split} \end{equation*}

\begin{equation*} \begin{split} & \sin 180^\text{o} = \sin (90^\text{o} + 90^\text{o}) \\\\ & \sin 180^\text{o} = \cos 90^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 180^\text{o} = 0} \end{split} \end{equation*}

3. Sudut di kuadran III (\(180^\text{o} < \alpha < 270^\text{o}\))

Menggunakan \((180^\text{o} + \alpha)\)	Menggunakan \((270^\text{o} - \alpha)\)
\begin{equation} \begin{split} & \sin 225^\text{o} = \sin (180^\text{o} + 45^\text{o}) \\\\ & \sin 225^\text{o} = − \sin 45^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 225^\text{o} = − \tfrac 12 \sqrt{2}} \end{split} \end{equation} 225º berada di kuadran III, maka sin 225º bernilai negatif.	\begin{equation} \begin{split} & \sin 225^\text{o} = \sin (270^\text{o} - 45^\text{o}) \\\\ & \sin 225^\text{o} = − \cos 45^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 225^\text{o} = − \tfrac 12 \sqrt{2}} \end{split} \end{equation} 225º berada di kuadran III, maka sin 225º bernilai negatif.
\begin{equation} \begin{split} & \cos 225^\text{o} = \cos (180^\text{o} + 45^\text{o}) \\\\ & \cos 225^\text{o} = - \cos 45^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\cos 225^\text{o} = - \tfrac 12 \sqrt{2}} \end{split} \end{equation} 225º berada di kuadran III, maka cos 225º bernilai negatif.	\begin{equation} \begin{split} & \cos 225^\text{o} = \cos (270^\text{o} - 45^\text{o}) \\\\ & \cos 225^\text{o} = - \sin 45^\text{o} \quad {\color {blue} \cos \rightarrow \sin}\\\\ & \bbox[5px, border: 2px solid magenta]{\cos 225^\text{o} = - \tfrac 12 \sqrt{2}} \end{split} \end{equation} 225º berada di kuadran III, maka cos 225º bernilai negatif.
\begin{equation} \begin{split} & \tan 225^\text{o} = \tan (180^\text{o} + 45^\text{o}) \\\\ & \tan 225^\text{o} = + \tan 45^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\tan 225^\text{o} = + 1} \end{split} \end{equation} 225º berada di kuadran III, maka tan 225º bernilai positif.	\begin{equation} \begin{split} & \tan 225^\text{o} = \tan (270^\text{o} - 45^\text{o}) \\\\ & \tan 225^\text{o} = + \cot 45^\text{o} \quad {\color {blue} \tan \rightarrow \cot}\\\\ & \bbox[5px, border: 2px solid magenta]{\tan 225^\text{o} = + 1} \end{split} \end{equation} 225º berada di kuadran III, maka tan 225º bernilai positif.
\begin{equation} \begin{split} & \sin 270^\text{o} = \sin (180^\text{o} + 90^\text{o}) \\\\ & \sin 270^\text{o} = -\sin 90^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 270^\text{o} = -1} \end{split} \end{equation} 270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.	\begin{equation} \begin{split} & \sin 270^\text{o} = \sin (270^\text{o} - 0^\text{o}) \\\\ & \sin 270^\text{o} = -\cos 0^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 270^\text{o} = -1} \end{split} \end{equation} 270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.

Menggunakan \((180^\text{o} + \alpha)\)

Menggunakan \((270^\text{o} - \alpha)\)

\begin{equation*} \begin{split} & \sin 225^\text{o} = \sin (180^\text{o} + 45^\text{o}) \\\\ & \sin 225^\text{o} = − \sin 45^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 225^\text{o} = − \tfrac 12 \sqrt{2}} \end{split} \end{equation*}

225º berada di kuadran III, maka sin 225º bernilai negatif.

\begin{equation*} \begin{split} & \sin 225^\text{o} = \sin (270^\text{o} - 45^\text{o}) \\\\ & \sin 225^\text{o} = − \cos 45^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 225^\text{o} = − \tfrac 12 \sqrt{2}} \end{split} \end{equation*}

225º berada di kuadran III, maka sin 225º bernilai negatif.

\begin{equation*} \begin{split} & \cos 225^\text{o} = \cos (180^\text{o} + 45^\text{o}) \\\\ & \cos 225^\text{o} = - \cos 45^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\cos 225^\text{o} = - \tfrac 12 \sqrt{2}} \end{split} \end{equation*}

225º berada di kuadran III, maka cos 225º bernilai negatif.

\begin{equation*} \begin{split} & \cos 225^\text{o} = \cos (270^\text{o} - 45^\text{o}) \\\\ & \cos 225^\text{o} = - \sin 45^\text{o} \quad {\color {blue} \cos \rightarrow \sin}\\\\ & \bbox[5px, border: 2px solid magenta]{\cos 225^\text{o} = - \tfrac 12 \sqrt{2}} \end{split} \end{equation*}

225º berada di kuadran III, maka cos 225º bernilai negatif.

\begin{equation*} \begin{split} & \tan 225^\text{o} = \tan (180^\text{o} + 45^\text{o}) \\\\ & \tan 225^\text{o} = + \tan 45^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\tan 225^\text{o} = + 1} \end{split} \end{equation*}

225º berada di kuadran III, maka tan 225º bernilai positif.

\begin{equation*} \begin{split} & \tan 225^\text{o} = \tan (270^\text{o} - 45^\text{o}) \\\\ & \tan 225^\text{o} = + \cot 45^\text{o} \quad {\color {blue} \tan \rightarrow \cot}\\\\ & \bbox[5px, border: 2px solid magenta]{\tan 225^\text{o} = + 1} \end{split} \end{equation*}

225º berada di kuadran III, maka tan 225º bernilai positif.

\begin{equation*} \begin{split} & \sin 270^\text{o} = \sin (180^\text{o} + 90^\text{o}) \\\\ & \sin 270^\text{o} = -\sin 90^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 270^\text{o} = -1} \end{split} \end{equation*}

270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.

\begin{equation*} \begin{split} & \sin 270^\text{o} = \sin (270^\text{o} - 0^\text{o}) \\\\ & \sin 270^\text{o} = -\cos 0^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 270^\text{o} = -1} \end{split} \end{equation*}

270º berada di kuadran III atau IV, maka sin 270º bernilai negatif.

4. Sudut di kuadran IV (\(270^\text{o} < \alpha < 360^\text{o}\))

Menggunakan \((360^\text{o} - \alpha)\)	Menggunakan \((270^\text{o} + \alpha)\)
\begin{equation} \begin{split} & \sin 300^\text{o} = \sin (360^\text{o} - 60^\text{o}) \\\\ & \sin 300^\text{o} = - \sin 60^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 300^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation} 300º berada di kuadran IV, maka sin 300º bernilai negatif.	\begin{equation} \begin{split} & \sin 300^\text{o} = \sin (270^\text{o} + 30^\text{o}) \\\\ & \sin 300^\text{o} = - \cos 30^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 300^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation} 300º berada di kuadran II, maka sin 300º bernilai positif.
\begin{equation} \begin{split} & \cos 300^\text{o} = \cos (360^\text{o} - 60^\text{o}) \\\\ & \cos 300^\text{o} = + \cos 60^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\cos 300^\text{o} = + \tfrac 12} \end{split} \end{equation} 300º berada di kuadran IV, maka cos 300º bernilai positif.	\begin{equation} \begin{split} & \cos 300^\text{o} = \cos (270^\text{o} + 30^\text{o}) \\\\ & \cos 300^\text{o} = + \sin 30^\text{o} \quad {\color {blue} \cos \rightarrow \sin}\\\\ & \bbox[5px, border: 2px solid magenta]{\cos 300^\text{o} = + \tfrac 12} \end{split} \end{equation} 300º berada di kuadran II, maka cos 300º bernilai negatif.
\begin{equation} \begin{split} & \tan 300^\text{o} = \tan (360^\text{o} - 60^\text{o}) \\\\ & \tan 300^\text{o} = - \tan 60^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\tan 300^\text{o} = - \sqrt{3}} \end{split} \end{equation} 300º berada di kuadran IV, maka tan 300º bernilai negatif.	\begin{equation} \begin{split} & \tan 300^\text{o} = \tan (270^\text{o} + 30^\text{o}) \\\\ & \tan 300^\text{o} = - \cot 30^\text{o} \quad {\color {blue} \tan \rightarrow \cot}\\\\ & \bbox[5px, border: 2px solid magenta]{\tan 300^\text{o} = - \sqrt{3}} \end{split} \end{equation} 300º berada di kuadran II, maka tan 300º bernilai negatif.

Menggunakan \((360^\text{o} - \alpha)\)

Menggunakan \((270^\text{o} + \alpha)\)

\begin{equation*} \begin{split} & \sin 300^\text{o} = \sin (360^\text{o} - 60^\text{o}) \\\\ & \sin 300^\text{o} = - \sin 60^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\sin 300^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation*}

300º berada di kuadran IV, maka sin 300º bernilai negatif.

\begin{equation*} \begin{split} & \sin 300^\text{o} = \sin (270^\text{o} + 30^\text{o}) \\\\ & \sin 300^\text{o} = - \cos 30^\text{o} \quad {\color {blue} \sin \rightarrow \cos}\\\\ & \bbox[5px, border: 2px solid magenta]{\sin 300^\text{o} = - \tfrac 12 \sqrt{3}} \end{split} \end{equation*}

300º berada di kuadran II, maka sin 300º bernilai positif.

\begin{equation*} \begin{split} & \cos 300^\text{o} = \cos (360^\text{o} - 60^\text{o}) \\\\ & \cos 300^\text{o} = + \cos 60^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\cos 300^\text{o} = + \tfrac 12} \end{split} \end{equation*}

300º berada di kuadran IV, maka cos 300º bernilai positif.

\begin{equation*} \begin{split} & \cos 300^\text{o} = \cos (270^\text{o} + 30^\text{o}) \\\\ & \cos 300^\text{o} = + \sin 30^\text{o} \quad {\color {blue} \cos \rightarrow \sin}\\\\ & \bbox[5px, border: 2px solid magenta]{\cos 300^\text{o} = + \tfrac 12} \end{split} \end{equation*}

300º berada di kuadran II, maka cos 300º bernilai negatif.

\begin{equation*} \begin{split} & \tan 300^\text{o} = \tan (360^\text{o} - 60^\text{o}) \\\\ & \tan 300^\text{o} = - \tan 60^\text{o} \\\\ & \bbox[5px, border: 2px solid magenta]{\tan 300^\text{o} = - \sqrt{3}} \end{split} \end{equation*}

300º berada di kuadran IV, maka tan 300º bernilai negatif.

\begin{equation*} \begin{split} & \tan 300^\text{o} = \tan (270^\text{o} + 30^\text{o}) \\\\ & \tan 300^\text{o} = - \cot 30^\text{o} \quad {\color {blue} \tan \rightarrow \cot}\\\\ & \bbox[5px, border: 2px solid magenta]{\tan 300^\text{o} = - \sqrt{3}} \end{split} \end{equation*}

300º berada di kuadran II, maka tan 300º bernilai negatif.

C. KOORDINAT KUTUB

Koordinat Cartesian

Rendered by QuickLaTeX.com

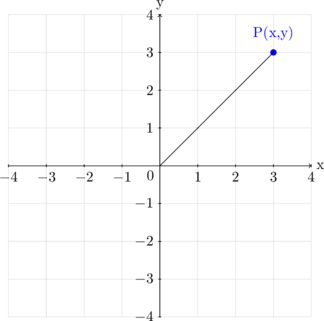
Menentukan koordinat Cartesian

\(x = r \:.\: \cos \theta\)

\(y = r \:.\: \sin \theta\)

Koordinat Kutub

Rendered by QuickLaTeX.com

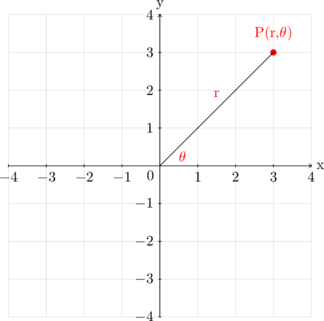
Menentukan koordinat kutub

\(r = \sqrt{x^2 + y^2}\)

\(\tan \theta = \dfrac yx\) → cek kuadran

TRIGONOMETRI

A. Segitiga Siku-siku B. Relasi Sudut C. Koordinat Kutub D. Persiapan Ulangan Kembali ke Modul SMA