A. FAKTORISASI
1. Bentuk \(ax^2 + bx = 0\)
\begin{equation*} \begin{split} & ax^2 + bx = 0 \\\\ & x \:.\: (ax + b) = 0 \\\\ & x = 0 \text{ atau } ax + b = 0 \end{split} \end{equation*}
Contoh
\begin{equation*} \begin{split} & x^2 - 5x = 0 \\\\ & x \:.\: (x - 5) = 0 \\\\ & \bbox[5px, border: 2px solid magenta]{x = 0 \text{ atau } x = 5} \end{split} \end{equation*}
2. Bentuk \(x^2 − a^2 = 0\)
\begin{equation*} \begin{split} & x^2 - a^2 = 0 \\\\ & (x + a) \:.\: (x - a) = 0 \\\\ & x + a = 0 \text{ atau } x - a = 0 \\\\ & x = -a \text{ atau } x = a \end{split} \end{equation*}
Contoh
\begin{equation*} \begin{split} & x^2 - 9 = 0 \\\\ & x^2 - 3^2 = 0 \\\\ & (x + 3)(x - 3) = 0 \\\\ & x + 3 = 0 \text{ atau } x - 3 = 0 \\\\ & \bbox[5px, border: 2px solid magenta]{x = -3 \text{ atau } x = 3} \end{split} \end{equation*}
3. Bentuk \(ax^2 + bx + c = 0\)
Lakukan cara trial and error (lihat contoh soal)
Contoh
\begin{equation*} \begin{split} & x^2 + 3x + 2 = 0 \\\\ & (x + 2)(x + 1) = 0 \\\\ & x + 2 = 0 \text{ atau } x + 1 & = 0 \\\\ & \bbox[5px, border: 2px solid magenta]{x = -2 \text{ atau } x = -1} \end{split} \end{equation*}
B. KUADRAT SEMPURNA
Rumus yang digunakan:
\((x + y)^2 = x^2 + 2 \:.\: x \:.\: y + y^2 \)
\((x - y)^2 = x^2 - 2 \:.\: x \:.\: y + y^2 \)
Contoh 01
Ubahlah bentuk \(x^2 + 6x + 7\) menjadi \((x + p)^2 + q\)
\begin{equation*} \begin{split} & x^2 + 6x + 7 \\\\ & (x + 3)^2 - 3^2 + 7 \\\\ & \bbox[5px, border: 2px solid magenta]{(x + 3)^2 - 2} \end{split} \end{equation*}
Contoh 02
Ubahlah bentuk \(x^2 - 8x + 20\) menjadi \((x + p)^2 + q\)
\begin{equation*} \begin{split} & x^2 - 8x + 20 \\\\ & (x - 4)^2 - 4^2 + 20 \\\\ & \bbox[5px, border: 2px solid magenta]{(x - 4)^2 + 4} \end{split} \end{equation*}
C. DISKRIMINAN
\(D = b^2 - 4ac\)
\(D > 0\), 2 akar real berbeda
\(D = 0\), 2 akar real yang sama (akar kembar)
\(D < 0\), tidak memiliki akar real (akar imaginer)
1. Bentuk definit positif
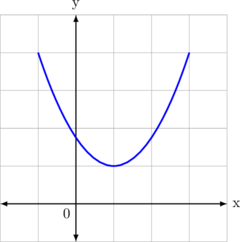
\(a^2 + bx + c > 0\)
Syarat:
\(\bbox[10px, border: 2px solid red]{a > 0 \text{ dan }D < 0}\)
Karena kurva membuka ke atas, maka \(a > 0\)
Karena kurva tidak memotong sumbu X, maka \(D < 0\)
2. Bentuk definit negatif
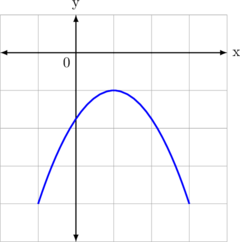
\(a^2 + bx + c < 0\)
Syarat:
\(\bbox[10px, border: 2px solid red]{a < 0 \text{ dan }D < 0}\)
Karena kurva membuka ke bawah, maka \(a < 0\)
Karena kurva tidak memotong sumbu X, maka \(D < 0\)
D. HUBUNGAN AKAR-AKAR
Persamaan kuadrat \(ax^2 + bx + c \ =\) memiliki akar-akar \(x_1\) dan \(x_2\), maka:
- \(x_1 + x_2 = - \dfrac{b}{a}\)
- \(x_1 \:.\: x_2 = \dfrac{c}{a}\)
- \(x_1 - x_2 = - \dfrac{\sqrt{D}}{a}\), untuk \(x_1 > x_2\)
Membentuk Persamaan Kuadrat Baru
Persamaan kuadrat yang memiliki akar-akar \(\alpha\) dan \(\beta\) dapat dibentuk dengan cara:
Cara 1
\(\bbox[10px, border: 2px solid red]{(x - \alpha)(x - \beta) = 0}\)
Cara 2
\(\bbox[10px, border: 2px solid red]{x^2 - (\alpha + \beta)x + \alpha \:.\: \beta = 0}\)
