SKETSA GRAFIK FUNGSI LINEAR
| No | Persamaan | Grafik |
|---|---|---|
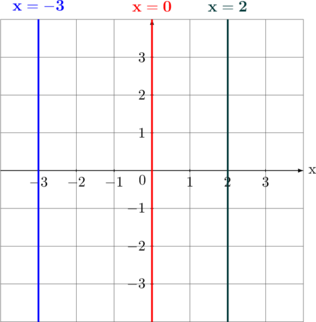
| 1 | \(x = -3\)
\(x = 0\)
\(x = 2\) |
|
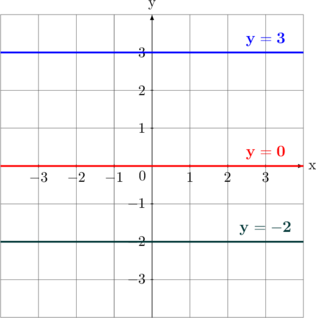
| 2 | \(y = 3\)
\(y = 0\)
\(y = -2\) |
|
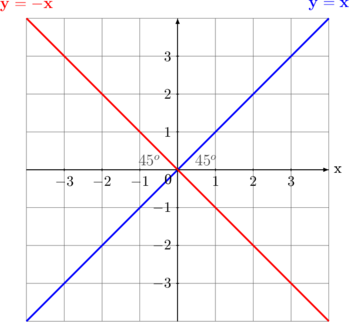
| 3 | \(y = x\) |
|
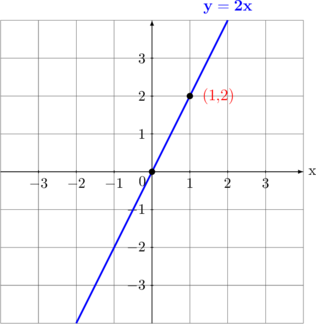
| 4 | \(y = 2x\)
Untuk \(x = 0 \rightarrow y = 0 \quad (0,0)\) Untuk \(x = 1 \rightarrow y = 2 \quad (1,2)\)
Garis melalui titik \((0,0)\) dan \((1,2)\) |
|
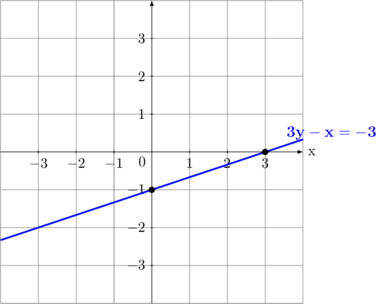
| 5 | \(y = \dfrac{1}{3}x - 1\)
Untuk \(x = 0 \rightarrow y = -1 \quad (0,-1)\) Untuk \(y = 0 \rightarrow x = 3 \quad (3,0)\)
Garis melalui titik \((0,-1)\) dan \((3,0)\) |
|
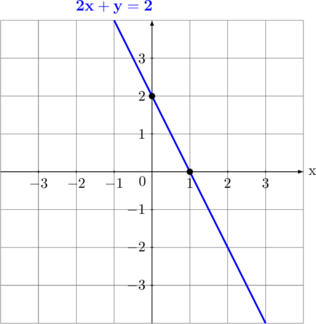
| 6 | \(2x + y = 2\)
Untuk \(x = 0 \rightarrow y = 2 \quad (0,2)\) Untuk \(y = 0 \rightarrow x = 1 \quad (1,0)\)
Garis melalui titik \((0,2)\) dan \((1,0)\) |
|
MENENTUKAN PERSAMAAN GARIS
| No | Keterangan | Rumus |
|---|---|---|
| 1 | Menentukan gradien | \(m = \dfrac {y_2 - y_1}{x_2 - x_1}\)
\(m = \tan \alpha\) |
| 2 | Diketahui titik \((a,0)\) dan \((0,b)\) | \(\dfrac xa + \dfrac yb = 1\) |
| 3 | Diketahui gradien dan titik \((x_1,y_1)\) | \(y - y_1 = m \:.\: (x - x_1)\) |
| 4 | Diketahui dua titik \((x_1,y_1)\) dan \((x_2,y_2)\) | \(\dfrac {y - y_1}{y_2 - y_1} = \dfrac {x - x_1}{x_2 - x_1}\) |
| 5 | Dua garis sejajar | \(m_1 = m_2\) |
| 6 | Dua garis saling tegak lurus | \(m_1 \:.\: m_2 = -1\) |