A. HUKUM TERMODINAMIKA
1. Sistem Dan Lingkungan
Sistem adalah aktivitas yang terjadi di dalam suatu materi, sedangkan lingkungan adalah hal-hal yang berada di luar sistem.
Hubungan antara sistem dan lingkungan dapat dibedakan menjadi:
Sistem terbuka
Dapat terjadi pertukaran massa dan energi
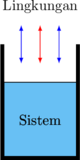
Sistem tertutup
Dapat terjadi pertukaran energi
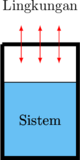
Sistem terisolasi
Tidak dapat terjadi pertukaran massa dan energi

2. Hukum I Termodinamika
Total energi dari sistem dan lingkungan tidak berubah. Energi dapat berpindah dari sistem ke
lingkungan atau sebaliknya. Energi juga dapat berubah wujud dalam bentuk usaha/kerja.
Hukum I Termodinamika pada dasarnya adalah hukum kekekalan energi.
Persamaan
\(\bbox[10px, border: 2px solid red] {\Delta U = Q - W}\)
ΔU: perubahan energi dalam (energi yang dimiliki oleh sistem)
Q: kalor (energi panas) yang masuk ke dalam sistem
W: kerja yang dilakukan oleh sistem
Penentuan tanda (+) dan (−) dari persamaan di atas dapat menggunakan pemahaman berikut:
(1) Energi dalam (ΔU)
Energi dalam bertambah, ΔU = +
Energi dalam berkurang, ΔU = −
(2) Kalor (Q)
Bila kalor (Q) masuk ke dalam sistem, akan membuat ΔU bertambah, sehingga Q = +
Bila kalor (Q) keluar dari sistem, akan membuat ΔU berkurang, sehingga Q = −
(3) Kerja (W)
Bila sistem melakukan kerja (W), akan membuat ΔU berkurang, sehingga W = +
Bila pada sistem dilakukan kerja, akan membuat ΔU bertambah, sehingga W = −
3. Hukum II Termodinamika
Pada suatu proses alami (spontan), perubahan entropi sistem selalu bernilai positif.
Dengan kata lain, entropi sistem selalu meningkat dengan berjalannya waktu.
Secara sederhana, entropi dapat diartikan sebagai tingkat ketidakteraturan suatu sistem. Semakin besar entropi, semakin tidak teratur sebuah sistem.
Contoh:
Es batu akan mencair (secara spontan) bila dimasukkan ke dalam air panas. Kalor mengalir dari air panas menuju es batu secara spontan, dan tidak mungkin terjadi sebaliknya.
Entropi es batu yang mencair lebih besar daripada entropi es batu (sebelum mencair).
4. Hukum III Termodinamika
Entropi sistem mencapai nilai maksimum pada suhu 0 K (−273ºC)
Hukum II Termodinamika menyatakan bahwa entropi sistem akan selalu meningkat. Namun entropi akan mencapai nilai tertentu yang mendekati angka 0 (tidak meningkat lagi) pada suhu 0 K (−273ºC).
Entropi sebuah sistem bernilai negatif. Saat entropi meningkat, nilainya semakin mendekati angka 0. Entropi akan mencapai nilai 0 pada saat suhu sistem 0 K (−273ºC).
Dengan kata lain, setiap benda akan mengalami stagnasi (partikel di dalam sistem tidak lagi mengalami perubahan) pada suhu 0 K (−273ºC).
B. ENERGI DALAM DAN USAHA
1. Energi Dalam
Energi dalam adalah total energi kinetik dari atom-atom atau molekul-molekul yang bergerak dalam suatu sistem.
Energi dalam
\(U = \dfrac 12 \:.\: f \:.\: n \:.\: R \:.\: T \)
\(U = \dfrac 12 \:.\: f \:.\: N \:.\: k \:.\: T\)
\(U = \dfrac 12 \:.\: f \:.\: P \:.\: V\)
Perubahan energi dalam
\(\Delta U = \dfrac 12 \:.\: f \:.\: n \:.\: R \:.\: \Delta T \)
\(\Delta U = \dfrac 12 \:.\: f \:.\: N \:.\: k \:.\: \Delta T\)
\(\Delta U = \dfrac 12 \:.\: f \:.\: (P_2 \:.\: V_2 - P_1 \:.\: V_1)\)
\(U\) = energi dalam
\(n\) = jumlah mol gas
\(N\) = jumlah atom/molekul gas
\(T\) = suhu (K)
\(f\) : dejarat kebebasan
Nilai derajat kebebasan pada suhu normal:
Gas monoatomik → \(f = 3\) (tiga dimensi)
Gas diatomik → \(f = 5\) (tiga dimensi dan dua arah rotasi)
Gas non linier triatomik → \(f = 6\)
\(R = 8,314 \text{ J/mol K}\)
\(k = 1,38 × 10^{-23} \text{ J/K}\)
2. Usaha
Besarnya usaha pada sistem ditentukan oleh:
\(\bbox[10px, border: 2px solid red] {\displaystyle W = \int_{V_1}^{V_2} P \: dV}\)
Isobarik (tekanan tetap)
\(\bbox[10px, border: 2px solid red] {W = P \:.\: (V_2 - V_1)}\)
Isokhorik (volume tetap)
\(\bbox[10px, border: 2px solid red] {W = 0}\)
Isotermik (suhu tetap)
\(\bbox[10px, border: 2px solid red] {W = n \:.\: R \:.\: T \:.\: \ln \left( \dfrac {V_2}{V_1} \right)}\)
3. Grafik P vs V
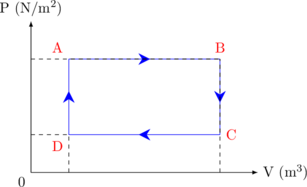
Proses A → B: sistem melakukan usaha
Proses B → C: tidak ada usaha yang dilakukan
Proses c → D: pada sistem dilakukan usaha
Proses D → A: tidak ada usaha yang dilakukan
Pada grafik P vs V, besarnya Kerja (W) dapat ditentukan dengan menghitung luas di bawah kurva.
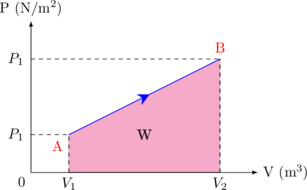
W = Luas Daerah di Bawah Kurva
C. PROSES TERMODINAMIKA
Proses termodinamika adalah aktivitas yang menyebabkan perubahan tekanan, volume dan suhu pada gas di dalam sistem. Proses termodinamika juga disertai oleh perubahan energi dalam (ΔU), kalor (Q) dan kerja (W).
1. Proses isobarik (tekanan tetap)
Persamaan
\begin{equation*} \begin{split} \frac {P_1 \:.\: V_1}{T_1} & = \frac {P_2 \:.\: V_2}{T_2} \\\\ \frac {\cancel {P_1} \:.\: V_1}{T_1} & = \frac {\cancel {P_2} \:.\: V_2}{T_2} \\\\ \frac {V_1}{T_1} & = \frac {V_2}{T_2} \end{split} \end{equation*}
Grafik P vs V
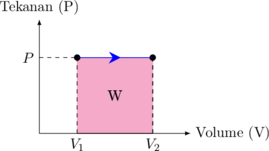
W = luas area di bawah grafik
Usaha
\begin{equation*} \begin{split} W & = P \:.\: \Delta V \\\\ W & = P \:.\: (V_2 - V_1) \end{split} \end{equation*}
2. Proses isokhorik (volume tetap)
Persamaan
\begin{equation*} \begin{split} \frac {P_1 \:.\: V_1}{T_1} & = \frac {P_2 \:.\: V_2}{T_2} \\\\ \frac {P_1 \:.\: \cancel {V_1}}{T_1} & = \frac {P_2 \:.\: \cancel {V_2}}{T_2} \\\\ \frac {P_1}{T_1} & = \frac {P_2}{T_2} \end{split} \end{equation*}
Grafik P vs V
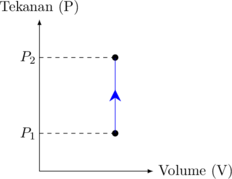
Usaha
Karena tidak ada perubahan volume, maka:
\(W = 0\)
Persamaan Termodinamika
Pada proses isokhorik, \(W = 0\), maka:
\begin{equation*} \begin{split} \Delta U & = Q - W \\\\ \Delta U & = Q - 0 \\\\ \Delta U & = Q \end{split} \end{equation*}
3. Proses isothermik (suhu tetap)
Persamaan
\begin{equation*} \begin{split} \frac {P_1 \:.\: V_1}{T_1} & = \frac {P_2 \:.\: V_2}{T_2} \\\\ \frac {P_1 \:.\: V_1}{\cancel {T_1}} & = \frac {P_2 \:.\: V_2}{\cancel {T_2}} \\\\ P_1 \:.\: V_1 & = P_2 \:.\: V_2 \end{split} \end{equation*}
Grafik P vs V

Usaha
\begin{equation*} W = n \:.\: R \:.\: T \:.\: \ln \left(\frac {V_2}{V_1} \right) \end{equation*}
Persamaan Termodinamika
Karena pada proses isothermik tidak ada perubahan suhu, maka tidak terjadi perubahan energi dalam, \(\Delta U = 0\)
\begin{equation*} \begin{split} \Delta U & = Q - W \\\\ 0 & = Q - W \\\\ Q & = W \end{split} \end{equation*}
4. Proses Adiabatik (Q = 0)
Proses adiabatik adalah proses yang berlangsung dimana sistem terisolasi, sehingga tidak ada massa dan kalor (Q) yang dapat masuk atau keluar dari sistem.
Persamaan
\begin{equation*} \begin{split} P \:.\: V^\gamma & = \text{konstan} \\\\ T \:.\: V^{\gamma - 1} & = \text{konstan} \\\\ P^{1 - \gamma} \:.\: T^{\gamma} & = \text{konstan} \end{split} \end{equation*}
\(\gamma\) = konstanta Laplace
\begin{equation*} \gamma = 1 + \frac 2f, \: \text{f adalah derajat kebebasan} \end{equation*}
Gas monoatomik memiliki 3 derajat kebebasan (3 dimensi)
Gas diatomik memiliki 5 derajat kebebasan (3 derajat kebebasan dan 2 arah rotasi)
Gas triatomik non linear memiliki 6 derajat kebebasan
Grafik P vs V

Usaha
\begin{equation*} W = \frac {1}{1 - \gamma} \:.\: (P_2 \:.\: V_2 - P_1 \:.\: V_1) \end{equation*}
Persamaan Termodinamika
Karena proses adiabatik merupakan sistem yang terisolasi, maka tidak ada kalor (Q) yang masuk atau keluar dari sistem,
\(Q = 0\)
\begin{equation*} \begin{split} \Delta U & = Q - W \\\\ \Delta U & = 0 - W \\\\ \Delta U & = - W \end{split} \end{equation*}
D. SIKLUS CARNOT
Siklus Carnot merupakan siklus termodinamika yang digunakan untuk mengubah energi panas menjadi usaha dengan efisiensi yang paling maksimum.
Siklus Carnot dapat digambarkan sebagai berikut:
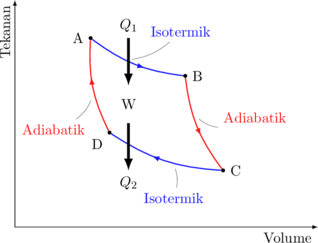
Proses A → B
- merupakan proses isotermik pada suhu \(T_1\)
- sistem menerima kalor dari luar (\(Q_1\))
Proses B → C
- merupakan proses adiabatik
- suhu sistem turun dari \(T_1\) ke \(T_2\)
Proses C → D
- merupakan proses isotermik pada suhu \(T_2\)
- sistem melepaskan kalor (\(Q_2\))
Proses D → A
- merupakan proses isotermik
- suhu sistem naik dari \(T_2\) ke \(T_1\)
Kerja pada siklus Carnot
Kerja yang dihasilkan merupakan selisih dari kalor yang diterima dan kalor yang dilepaskan.
\(\bbox[10px, border: 2px solid red] {W = Q_1 - Q_2}\)
\(\bbox[10px, border: 2px solid red] {\dfrac {Q_1}{Q_2} = \dfrac {T_1}{T_2}}\)
Efisiensi pada siklus Carnot
Efisiensi merupakan kerja yang dihasilkan dibandingkan dengan input yang diterima.
\(\bbox[10px, border: 2px solid red] {\eta = \dfrac {W}{Q_1} \times 100\% \quad {\color {blue} \dotso \: (1)}}\)
\begin{equation*} \begin{split} & \eta = \dfrac {Q_1 - Q_2}{Q_1} \times 100\% \\\\ & \bbox[10px, border: 2px solid red] {\eta = \left(1 - \frac {Q_2}{Q_1}\right) \times 100\% \quad {\color {blue} \dotso \: (2)}} \end{split} \end{equation*}
\(\bbox[10px, border: 2px solid red] {\eta = \left(1 - \dfrac {T_2}{T_1}\right) \times 100\% \quad {\color {blue} \dotso \: (3)}}\)
