A. USAHA DAN ENERGI
Usaha adalah perkalian titik (dot product) dari vektor gaya (F) dan vektor perpindahan (S)
\(\bbox[10px, border: 2px solid red]{W = \overrightarrow {F} \cdot \overrightarrow {S}}\)
- Usaha merupakan besaran skalar (tidak memiliki arah)
- Usaha dapat bernilai (+), (−) atau NOL
-
- Usaha bernilai (+) bila arah gaya searah dengan arah perpindahannya
- Usaha bernilai (−) bila arah gaya berlawanan dengan arah perpindahannya
- Usaha bernilai NOL bila tidak menghasilkan perpindahan atau arah gaya tegak lurus terhadap arah perpindahan
-
Usaha bernilai positif
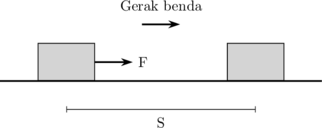
\(W = F \:.\: S\)
Usaha bernilai positif

\(W = F \cos \alpha \:.\: S\)
Usaha bernilai negatif
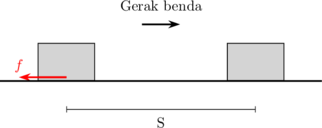
\(W = - f \:.\: S\)
Usaha bernilai nol
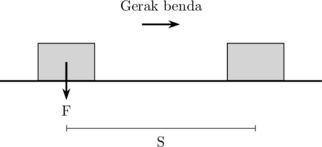
\(W = 0\)
Pada grafik F vs S, besar usaha dapat ditentukan dengan menghitung luas dari daerah yang dibatasi oleh grafik dan sumbu X.

Hubungan Usaha Dan Energi
Usaha dan Energi Kinetik
\begin{equation*} \begin{split} & \bbox[10px, border: 2px solid red]{W_{\text{gaya luar}} = \Delta EK} \\\\ & W_{\text{gaya luar}} = EK_2 - EK_1 \\\\ & W_{\text{gaya luar}} = \tfrac{1}{2} \:.\: m \:.\: (v_2^2 - v_1^2) \end{split} \end{equation*}
Usaha dan Energi Potensial Gravitasi
\begin{equation*} \begin{split} & \bbox[10px, border: 2px solid red]{W_{\text{gravitasi}} = - \Delta EP} \\\\ & W_{\text{gravitasi}} = - (EP_2 - EP_1) \\\\ & W_{\text{gravitasi}} = - m \:.\: g \:.\: (h_2 - h_1) \\\\ & W_{\text{gravitasi}} = m \:.\: g \:.\: (h_1 - h_2) \end{split} \end{equation*}
Usaha dan Energi Potensial Pegas
\begin{equation*} \bbox[10px, border: 2px solid red]{W_{\text{pegas}} = \frac{1}{2} \:.\: k \:.\: (\Delta x)^2} \end{equation*}
B. HUKUM KEKEKALAN ENERGI
Energi Potensial Gravitasi
\(E_P = m \:.\: g \:.\: h\)
Energi Kinetik
\(E_K = \frac{1}{2} \:.\: m \:.\: v^2\)
Energi Mekanik
\(\bbox[10px, border: 2px solid red]{E_M = E_P + E_K}\)
\(E_M = m \:.\: g \:.\: h + \frac{1}{2} \:.\: m \:.\: v^2\)
Energi Potensial Pegas
\(E_K = \frac{1}{2} \:.\: k \:.\: (\Delta x)^2\)
Hukum Kekekalan Energi Mekanik
\(\bbox[10px, border: 2px solid red]{E_{M1} = E_{M2}}\)
\(E_{P1} + E_{K1} = E_{P2} + E_{K2}\)
Hukum Kekekalan Energi Mekanik berlaku jika tidak ada gaya luar (usaha luar) yang bekerja
Contoh

\begin{equation*} \begin{split} & E_{M1} = E_{M2} \\\\ & E_{P1} + E_{K1} = E_{P2} + E_{K2} \\\\ & m \:.\: g \:.\: h_1 + \tfrac{1}{2} \:.\: m \:.\: v_1^2 = m \:.\: g \:.\: h_2 + \tfrac{1}{2} \:.\: m \:.\: v_2^2 \\\\ & \cancel {m} \:.\: g \:.\: h_1 + \tfrac{1}{2} \:.\: \cancel {m} \:.\: v_1^2 = \cancel {m} \:.\: g \:.\: h_2 + \tfrac{1}{2} \:.\: \cancel {m} \:.\: v_2^2 \\\\ & g \:.\: h_1 + \tfrac{1}{2} \:.\: v_1^2 = g \:.\: h_2 + \tfrac{1}{2} \:.\: v_2^2 \end{split} \end{equation*}
Jika ada gaya luar (usaha luar) yang bekerja:
\(\bbox[10px, border: 2px solid red]{W_{\text{gaya luar}} = E_{M2} - E_{M1}} \)
\( F \:.\: S = (E_{P2} + E_{K2}) - (E_{P1} + E_{K1}) \)
C. DAYA DAN EFISIENSI
Daya
\(\bbox[10px, border: 2px solid red]{P = \dfrac {\text{Usaha}}{\text{waktu}} = \dfrac{W}{t} \quad \dotso \text{ Watt}}\)
Efisiensi
\(\bbox[10px, border: 2px solid red]{\eta = \dfrac{P_{\text{output}}}{P_{\text{input}}} \times 100\%}\)
