A. PENJUMLAHAN VEKTOR
1. Metode Poligon
Resultan vektor dapat ditentukan dengan metode poligon, yaitu menyusun vektor-vektor saling berurutan sehingga membentuk poligon.
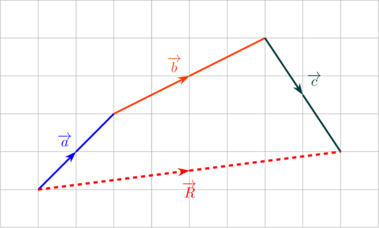
\(\overrightarrow R = \overrightarrow a + \overrightarrow b + \overrightarrow c\)
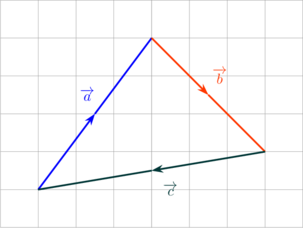
\(\overrightarrow a + \overrightarrow b + \overrightarrow c = 0\)
Jika beberapa vektor tersusun saling berturutan hingga kembali ke titik awal, jumlah seluruh vektor akan sama dengan nol.
2. Metode Jajargenjang
Jumlah dan selisih dua vektor juga dapat ditentukan dengan metode jajaran genjang.
Diketahui dua buah vektor \(\overrightarrow a\) dan \(\overrightarrow b\) saling membentuk sudut \(\theta\) seperti gambar di bawah ini:
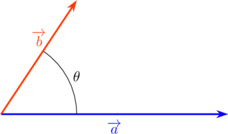
(A) resultan kedua vektor \(\overrightarrow a + \overrightarrow b\)
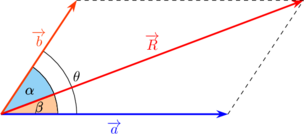
\( R = |a + b| = \sqrt{a^2 + b^2 + 2 \: a \: b \cos \theta}\)
\(\dfrac{|a|}{\sin \alpha} = \dfrac{|b|}{\sin \beta} = \dfrac{|R|}{\sin \theta}\)
(B) selisih kedua vektor \(\overrightarrow a - \overrightarrow b\)
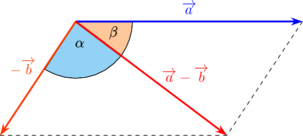
\( |a - b| = \sqrt{a^2 + b^2 - 2 \: a \: b \cos \theta}\)
\(\dfrac{|a|}{\sin \alpha} = \dfrac{|b|}{\sin \beta} = \dfrac{|a - b|}{\sin \theta}\)
3. Metode Komponen Vektor
Sebuah vektor dapat diurai menjadi dua vektor (komponen arah x dan komponen arah y)
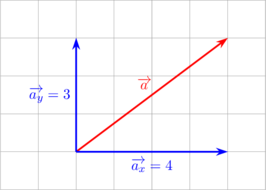
\(\overrightarrow a_x = 4\) dan \(\overrightarrow a_y = 3\)
\(\overrightarrow a = 4 \: \overrightarrow i + 3 \: \overrightarrow j\)
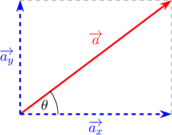
\(\cos \theta = \dfrac {\overrightarrow {a_x}}{a} \rightarrow \overrightarrow {a_x} = \overrightarrow a \:.\: \cos \theta\)
\(\sin \theta = \dfrac {\overrightarrow {a_y}}{a} \rightarrow \overrightarrow {a_y} = \overrightarrow a \:.\: \sin \theta\)
Menentukan resultan dengan metode komponen vektor
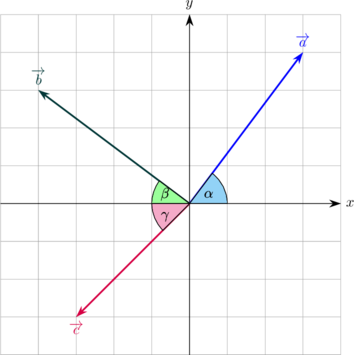
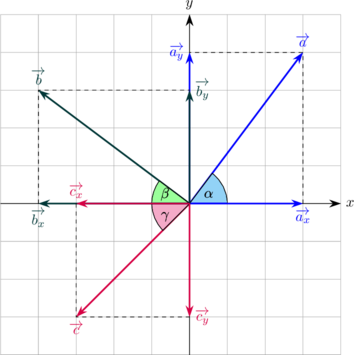
Vektor Komponen arah X Komponen arah Y
\(\overrightarrow a\) \(\overrightarrow a_x = a \cos \alpha\) \(\overrightarrow a_y = a \sin \alpha\)
\(\overrightarrow b\) \(\overrightarrow b_x = -b \cos \beta\) \(\overrightarrow b_y = b \sin \beta\)
\(\overrightarrow c\) \(\overrightarrow c_x = -c \cos \gamma\) \(\overrightarrow c_y = -c \sin \gamma\)
\(\Sigma \overrightarrow X = \overrightarrow a_x + \overrightarrow b_x + \overrightarrow c_x\) \(\Sigma \overrightarrow Y = \overrightarrow a_y + \overrightarrow b_y + \overrightarrow c_y\)
\(|R| = \sqrt{(\Sigma \overrightarrow X)^2 + (\Sigma \overrightarrow Y)^2} \quad \tan \theta = \dfrac{\Sigma \overrightarrow Y}{\Sigma \overrightarrow X} \)
Catatan:
(tanda − ditambahkan pada komponen \(\overrightarrow b_x, \: \overrightarrow c_x\) dan \(\overrightarrow c_y\) karena ke arah x negatif dan y negatif.
B. PERKALIAN VEKTOR
