Intersection and Union

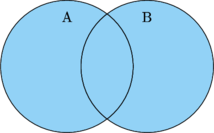
The intersection of two sets A and B is the set of elements common to both A and B. The symbol is "\(\cap\)"

\(\text{A}\cap\text{B}\)

The union of two sets A and B is the set of elements in A or B (or both). The symbol is "\(\cup\)"

\(\text{A}\cup\text{B}\)

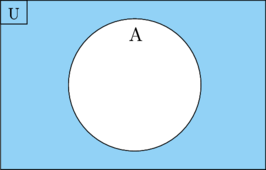
Complement Set

Given a set A, the complement of A is the set off all elements in the universal set U, but not in A. We can write \(\text{A}^{\text{c}}\)

Properties of Set Operation

A. Commutative

\(\text{A}\cap\text{B} = \text{B}\cap\text{A}\) \(\text{A}\cup\text{B} = \text{B}\cup\text{A}\)

B. Distributive

\(\text{A}\cup(\text{B}\cap\text{C}) = (\text{A}\cup \text{B})\cap (\text{A}\cup\text{C})\)

\(\text{A}\cap(\text{B}\cup\text{C}) = (\text{A}\cap \text{B})\cup (\text{A}\cap\text{C})\)

C. De'Morgan Theorem

\((\text{A}\cup\text{B})^{\text{c}} = \text{A}^{\text{c}} \cap \text{B}^{\text{c}}\) \((\text{A}\cap\text{B})^{\text{c}} = \text{A}^{\text{c}} \cup \text{B}^{\text{c}}\)