A set is a collection of well-defined objects

A set is well-defined if we are able to tell whether or not any particular object is an element of the set

 

Example:

Which of the following are well-defined sets?

(1)   All the tall girls of the school

(2)   All the letters in the word "mathematics"

(3)   All the hardworking teachers in a school

(4)   All the honest members in the family

Answer: (2)

All the letters in the word "mathematics" is well-defined sets

B = {m, a, t, h, e, i, c, s}

 

The following conventions are used with sets:

• Capital letters are used to denote sets
• Curly braces { } denote a list of elements in a set
• Lowercase letters are used to denote elements of sets

Example:

A is the set of vowels

A = {a, i, u, e, o}

 

The elements in the sets are depicted in either the statement form, set-builder notation form or roster form

1. Statement form

A = {prime numbers between 10 and 30}

2. Set-builder notation

A = {x| 10 < x < 30, x ∈ prime numbers}

We read it as, "A is the set of all x such that x is more than10 but less than 30 and x belongs to prime numbers"

3. Roster form

A = {11, 13, 17, 19, 23, 29}

 

Elements Of a Set

An element is a member of a set.

Notation:

∈  means “is an element of”

∉  means “is not element of”

 

Cardinality

The number of elements of a set is expressed as n(A)

 

Example:

A = {positive integers between −3 and 3}

A = {1, 2}

1 ∈ A  {1 is an element of A}

2 ∈ A  {2 is an element of A}

3 ∉ A {3 is not element of A}

n(A) = 2

 

Empty Set and Infinite Set

Null or empty set 

Set with no elements 

Example:

The sets of triangles having 4 sides

It is an empty set, because every triangle has 3 sides

 

Infinite set

The element cannot be listed (unlimited)

Example:

• Set of all point in a line segment
• Set of all natural numbers
• Set of all integers

 

Subset

$\text{A}$ is a subset of $\text{A}$ ($\text{A}\subseteq \text{B}$) if and only if every element of $\text{A}$ is in $\text{B}$.

The total number of subsets of a set with n elements is $2^n$.

Example:

$\text{P}=\{5,10,15,20\}$

$\text{Q}=\{5,10,15,20,25,30\}$

$\text{P}$ is a proper subset of $\text{Q}$ because the element 25 and 30 is not in the set $\text{P}$. ($\text{P}\subset \text{Q}$)

The number of subset of $\text{Q}$ is $2^6=64$.

 

Example:

Find the number of subsets of  $\text{P}=\{\text{a, b, c, d, e, f}\}$  that contain exactly 3 elements

 

The total number of subsets of $\text{P}$ is $2^6$

Using Pascal's triangle:

 

So, the number of subsets of $\text{P}$ that contain exactly 3 elements is 20.

 

Equal Sets and Equivalent Sets

Two sets A and B are equal if they contain exactly the same elements

Example:

A = {1, 2, 4} and B = {4, 2, 1}

So set A is equal set B (A = B)

 

Two sets A and B are said to be equivalent if they have the same cardinality i.e. n(A) = n(B)

Example:

A = {a, i, u, e, o} and B = {2, 3, 5, 7, 11}

Set A is equivalent set B (A ∼ B) because n(A) = n(B) = 5

 

Universal Set

A universal set is the set of all elements or members of all related sets

Example :

Describe one possible universal set for each of the following sets!

1. {4, 6, 8, 10}

2. {Neptune, Saturn}

3. {cat, dog}

Solution:

1. U = the set of even numbers

2. U = the set of planets in our solar system

3. U = the set of pets

 

Disjoint Set and Joint Set

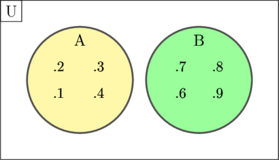
Disjoint set is two or more sets which have no elements in common

Example:

$\text{U}=\{1,2,3,4,6,7,8,9\}$

$\text{A}=\{1,2,3,4\}$

$\text{B}=\{6,7,8,9\}$

Set A and B are called disjoint set

 

 

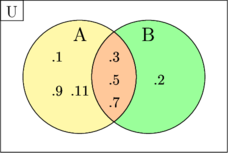
Joint set is two or more sets which have elements in common

Example:

$\text{U}=\{1,2,3,5,7,9,11\}$

$\text{A}=\{1,3,5,7,9,11\}$

$\text{B}=\{2,3,5,7\}$

Set A and B is joint set because they have elements in common {3, 5, 7}