Circumference of A Circle

\(\text{circumference of circle} = 2\times \pi\times r\)

\(\pi = \frac{22}{7} = 3.14\)

\(r = \text{radius}\)

\(\text{circumference of circle} =\pi\times d\)

\(d = \text{diameter}\)

Arc Length

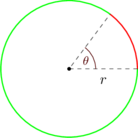
\(\text{If θ is measured in degrees then:}\)

\(\text{Arc length} = \frac{\theta}{360^\circ} \times \text{circumference of circle} \)

\(\text{Arc length} = \frac{\theta}{360^\circ} \times 2\times \pi \times r \)

\(\text{If θ is measured in radians then:}\)

\(\text{Arc length} = \theta \times r\)

\(1 \pi \text { radians} = 180^\circ\)

\(1 \text{ radians ≈  57.3°}\)