Circumference of A Circle

$\text{circumference of circle}=2\times \pi \times r$

$\pi =\frac{22}{7}=3.14$

$r=\text{radius}$

$\text{circumference of circle}=\pi \times d$

$d=\text{diameter}$

Arc Length

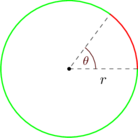
$\text{If θ is measured in degrees then:}$

$\text{Arc length}=\frac{\theta }{{360}^{\circ }}\times \text{circumference of circle}$

$\text{Arc length}=\frac{\theta }{{360}^{\circ }}\times 2\times \pi \times r$

$\text{If θ is measured in radians then:}$

$\text{Arc length}=\theta \times r$

$1\pi \text{ radians}={180}^{\circ }$

$1\text{ radians ≈ 57.3°}$